机器学习算法之数据降维

数据降维是通过某种数学变换将原始高维属性空间，转变为一个低维子空间，对数据进行降维，可以有效地去除样本中冗余的属性，减少数据容量，缓解维数灾难，加快学习速度。数据降维的常用方法有主成分分析(PCA)、多维缩放(MDS)、线性判别分析(LDA)、等度量映射(Isomap)、局部线性嵌入(LLE)、t分布随机邻域嵌入(t-SNE)、Laplacian Eigenmaps等。

主成分分析(PCA)

主成分分析是一种线性降维方法，将高维空间映射到低维空间，并使得所有样本在低维空间的投影点尽可能分开，也就是低维子空间对样本具有最大可分性，为了实现这种最大可分性，应该使投影后样本的方差最大化。

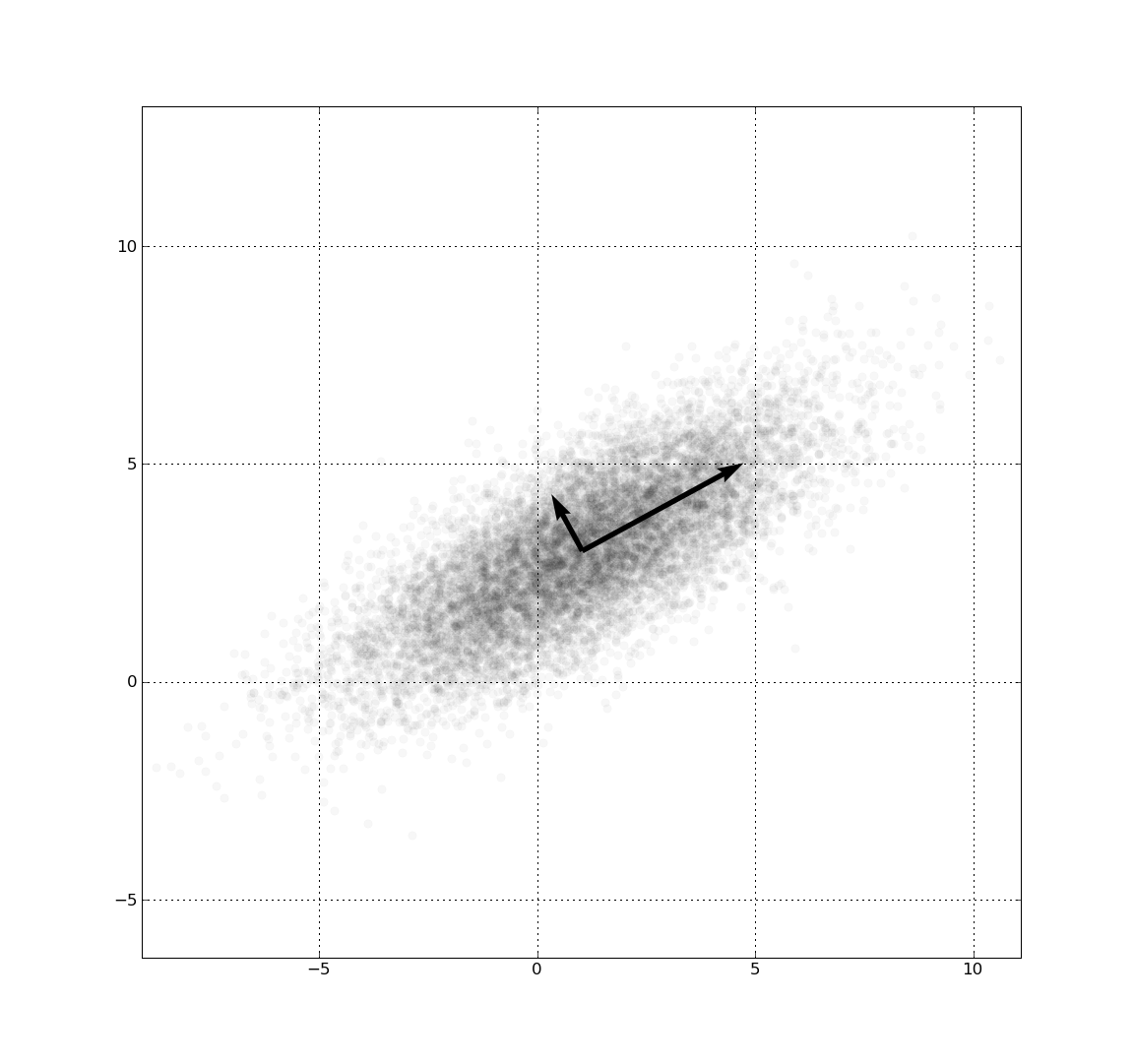
对于一个维数为$D$的高维空间，样本点$x_i=(x_1,x_2,…,x_D)$通过与矩阵$W$相乘映射到低维空间（维数为$d$，$d<D$）中的某个点$z_i=W^T x_i=(z_1,z_2,…,z_d)$，矩阵$W$的大小是$D\ast d$。令数据样本集的大小为$N$，PCA的目标是要让低维子空间中 $z_{i}$ 尽可能地分开，因此投影后样本的方差要尽可能的大。假定数据样本进行了中心化，数据每一维的均值为$0$，即 $\Sigma_{i}x_{i}=0$，乘上矩阵$W^T$得到的降维后的数据每一维均值也为$0$，考虑高维空间中原始样本数据集的协方差矩阵$C=\dfrac{1}{N}\ast XX^T$，协方差矩阵中对角线上的值为某一维的方差，非对角线上的值为两维之间的协方差。降维后低维子空间中相应的协方差矩阵为$B=\dfrac{1}{N}\ast ZZ^T$，如果希望降维后的点具有最大的可分性，那么协方差矩阵$B$对角线上的值也就是每一维的方差应该尽可能的大，同时为了让不同的属性能够更多地表示原始信息，而不包含冗余的信息，可以使不同属性之间正交，这种情况下矩阵$B$非对角线上的值即不同维之间的协方差为$0$。因此降维后的每一维既有足够的区分性，又能代表不同的信息。对于矩阵$B$，可进一步推导出$B=\dfrac{1}{N}\ast ZZ^T=\dfrac{1}{N}\ast W^T X(W^T X)^T=W^T (\dfrac{1}{N}\ast XX^T)W=W^TCW$，这个式子表明，线性变换矩阵$W$实现数据降维的过程是将高维空间中的协方差矩阵$C$对角化，因此可通过求协方差矩阵$C$的特征值以及对应的特征向量来确定投影变换矩阵$W$。PCA的算法流程如下所述：

输入：样本集${x_1,x_2,…,x_N }$，低维空间的维数$d$；
过程：
对所有数据样本进行中心化$x_i=x_i-\dfrac{1}{N} \Sigma_{i}x_{i}$；
计算样本的协方差矩阵$C=\dfrac{1}{N} XX^T$；
对协方差矩阵$C$做特征值分解：
取最大的$d$个特征值对应的特征向量$w_1,w_2,…,w_d$；
输出：投影矩阵$W=(w_1,w_2,…,w_d)$，$w_i$为$D$维列向量。

多维缩放(MDS)

多维缩放要求原始高维空间中数据样本之间的距离在低维空间中保持不变，即在降维的过程中保留原始数据的差异性。

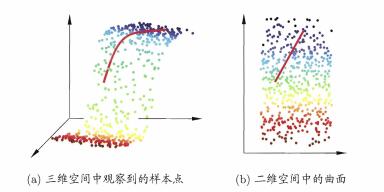
假定$N$个样本在$D$维原始空间的距离矩阵为$A\in R^{N×N}$，其第$i$行第$j$列的元素$a_{ij}$为样本$x_i$到$x_j$的距离。多维缩放的目标是获得数据样本在$d$维空间的表示$Z\in R^{d×N}$,$d≤D$，且任意两个样本在低维空间的欧氏距离等于原始空间中的距离，即$\left|z_i-z_j \right|=a_{ij}$。令$B=Z^T Z\in R^{N×N}$,其中$B$为降维后样本的內积矩阵，$b_{ij}=z_i^T z_j$，根据样本在原始空间和低维空间的距离相等有
$$a_{ij}^2=‖z_i-z_j ‖^2=‖z_i ‖^2+‖z_j ‖^2-2z_i^T z_j=b_{ii}+b_{jj}-2b_{ij}$$
令降维后的数据样本$Z$中心化，数据每一维的均值为$0$，即$\Sigma_i z_i = 0$。显然，內积矩阵$B$的行与列之和均为$0$，即$\Sigma_{i=1}^N b_{ij} = \Sigma_{j=1}^N b_{ij} = 0$，则有以下式子成立：
$$\Sigma_{i=1}^N a_{ij}^2 =tr(B)+Nb_{jj}$$
$$\Sigma_{j=1}^N a_{ij}^2 =tr(B)+Nb_{ii}$$
$$\Sigma_{i=1}^N \Sigma_{j=1}a_{ij}^2 =2Ntr(B)$$
其中 $tr(B)=\Sigma_{i=1}^N ‖z_i‖^2$ 为矩阵$B$的迹，令
$$a_{i\cdot}^2=\dfrac{1}{N} \Sigma_{j=1}^N a_{ij}^2$$
$$a_{\cdot j}^2=\dfrac{1}{N} \Sigma_{i=1}^N a_{ij}^2$$
$$a_{\cdot \cdot}^2=\dfrac{1}{N^2} \Sigma_{i=1}^N \Sigma_{j=1}^N a_{ij}^2$$
由以上各式可得
$$b_{ij}=-\dfrac{1}{2} (a_{ij}^2-a_{i \cdot}^2-a_{\cdot j}^2+a_{\cdot \cdot}^2)$$
由此即可通过降维前后保持不变的距离矩阵$A$求取內积矩阵$B$。对矩阵$B$做特征值分解，$B=VΛV^T$，其中$Λ=diag(λ_1,λ_2,…,λ_d)$为特征值构成的对角矩阵，$λ_1≥λ_2≥\ldots≥λ_d$，$V$为特征向量矩阵，则$Z$可表达为
$$Z=Λ^{1/2} V^T∈R^{d×N}$$
为了实现有效降维，往往仅需降维后的距离与原始空间中距离尽可能接近，而不必严格相等，因此可取$d(d<<D)$个最大特征值构成对角矩阵。MDS的算法流程如下所述：

输入：距离矩阵$A∈R^{N×N}$，其元素$a_{ij}$为样本$x_i$到$x_j$的距离，原始空间维数为$D$，低维空间维数为$d$；
过程：
计算內积矩阵$B$；
对矩阵$B$做特征值分解；
取$d$个最大的特征值构成的对角矩阵$Λ$和对应的特征向量矩阵$V$；
输出：矩阵$Z=Λ^{1/2} V^T∈R^{d×N}$，每列为一个样本的低维坐标。

线性判别分析(LDA)

线性判别分析是一种典型的线性学习方法，在二分类问题上最早由Fisher提出。LDA的基本思想是给定数据样本集，设法将样本投影到一个低维空间，使得同类样本的投影点尽可能接近，不同类样本的投影点尽可能远离。LDA和PCA的降维思路相似，都是通过矩阵乘法进行线性降维，但两者原理有所不同，PCA是希望所有样本在每一维上尽可能分开。

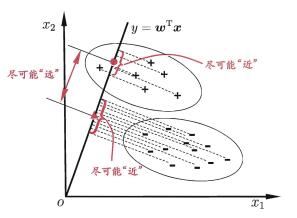
给定数据样本集$D={(x_i,y_i )},i=1,2,…,N$，样本集的大小为$N$，样本的类别数为$K$，令$X_i$ 、$μ_i$ 、$Σ_i$分别表示第$i(i=1,2,…,K)$类样本的集合、均值向量和协方差矩阵，样本在低维空间的表示为$z_i=W^T x_i$，欲使同类样本的投影点尽可能近，可以让同类样本投影点的协方差尽可能小；欲使不同类样本的投影点尽可能远离，则可以让不同类中心之间的距离尽可能大，定义类内散度矩阵
$$S_w=\Sigma_{k=1}^K S_k = \Sigma_{k=1}^K \Sigma_{X∈X_k} (X-μ_k)(X-μ_k)^T$$
即$K$个类的原始数据协方差矩阵相加。定义类间散度矩阵
$$S_b=\Sigma_{k=1}^K N_k (μ_k-u)(μ_k-u)^T$$
其中$μ=1/N \Sigma_{k=1}^K N_k μ_k$($N_k$为第$k$类的样本个数)，同时考虑两者，则LDA算法的最大化目标
$$max_W J(W)=tr(W^T S_b W)/tr(W^T S_w W)$$
其中，$W∈R^{D×(N-1)}$，$tr(∙)$表示矩阵的迹，$J(W)$对$W$求偏导
$$∂J(W)/∂W=(W^T S_w W)2S_b W-(W^T S_b W)2S_w W = 0$$
$$S_b W - J(W) S_w W = 0$$
上式表明$W$的闭式解是$S_w^{-1} S_b$的$K-1$最大广义个特征值所对应的特征向量组成的矩阵。若将$W$视为一个投影矩阵，则多分类LDA将样本投影到$K-1$维空间，$K-1$通常远小于数据的原有属性数。通过投影可有效减少样本的维数，而且投影过程中使用了类别信息，因此LDA也常视为一种经典的监督降维技术。LDA的算法流程如下：

输入：数据样本集$D={(x_i,y_i)},i=1,2,…,N$，数据可以分为$K$个类；
过程：
计算类内散度矩阵$S_w$和类间散度矩阵$S_b$；
对矩阵$S_w$做奇异值分解，$S_w=UΣV^T, S_w^{-1}=VΣ^{-1} U^T$，$Σ$是一个实对称矩阵；
对矩阵$S_w^{-1} S_b$进行特征值分解；
取最大的d个特征值对应的特征向量；
输出：$W=(w_1,w_2,…,w_d)$

等度量映射(Isomap)

等度量映射是一种基于流形学习的数据降维方法，流形是在局部与欧式空间同胚的空间，也就是说在局部具有欧式空间的性质，可以利用欧氏距离进行距离计算。低维流形嵌入到高维空间之后，直接在高维空间中计算直线距离具有误导性，因为高维空间中直线距离在低维嵌入流形上是不可达的。利用流形在局部上与欧式空间同胚的性质，对每个点基于欧式距离找出其近邻点，然后建立一个近邻连接图，图中近邻点之间存在连接，而非近邻点之间不存在连接。于是计算两点之间测地线距离的问题，就转变为计算近邻连接图上两点之间的最短路径问题，基于近邻逼近能获得低维流形上测地线很好的近似。

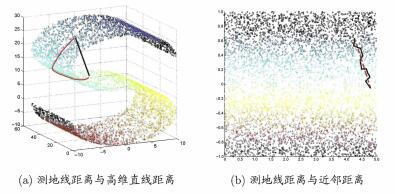
多维缩放(MDS)对数据降维，需要已知高维空间中样本之间的距离关系，等度量映射(Isomap)结合流形学习的思想和多维缩放的方法来进行降维，在高维空间的局部空间，计算邻近点的欧式距离，并构建近邻连接图。然后利用Dijkstra算法或Floyd算法在近邻连接图上计算两点间的最短路径，得到任意两点间的距离之后，即可作为MDS算法的输入距离矩阵，通过MDS算法输出样本在低维空间的投影。Isomap算法描述如下：

输入：数据样本集${x_1,x_2,…,x_N }$，近邻参数$k$，低维空间维数$d$；
过程：
利用$k$近邻算法计算$x_i$与$k$个近邻样本点的欧式距离，与其他点的距离设为无穷大；
根据最短路径算法计算任意两个样本点之间的距离，得到距离矩阵$A$；
将距离矩阵$A$作为MDS算法的输入，得到输出；
输出：样本集在低维空间的投影$Z=(z_1,z_2,…,z_N)$，$z_i$为低维空间的向量。

局部线性嵌入(LLE)

局部线性嵌入是一种基于流形学习的算法，能够使降维后的数据较好地保持原有的流形结构。与等度量映射(Isomap)试图保持近邻样本之间的距离不同，LLE试图保持降维前后邻域内样本之间的线性关系。

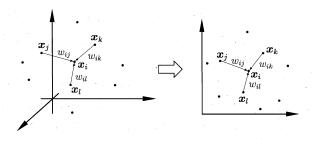
在原始空间中，假定样本点$x_i$的坐标利用其邻域样本的坐标通过线性组合而重构出来，即$x_i=\Sigma_{j∈X_i} w_{ij} x_j$，其中$X_i$是$x_i$邻域内样本点的下标集合。通过最小化重构误差来求解对每个样本点$x_i$进行线性重构的权值系数$w_i$，即
$$min_{w_1,w_2,…,w_m} \Sigma_{i=1}^m ‖x_i-\Sigma_{j∈X_i} w_{ij} x_j‖, s.t.\Sigma_(j∈X_i) w_{ij}=1$$
其中$x_i$和$x_j$均为已知样本点，定义局部协方差矩阵$C_{jk}=(x_i-x_j)^T (x_i-x_k )，w_{ij}$有闭式解
$$w_{ij}=(\Sigma_{k∈X_i} C_{jk}^{-1})/(\Sigma_{l,s∈X_i} C_{ls}^{-1})$$
LLE在低维空间中保持权重$w_i$不变，因此$x_i$对应在低维空间的坐标$z_i$可通过最优化下式求解
$$min_{z_1,z_2,…,z_m} \Sigma_{i=1}^m ‖z_i-\Sigma_{j∈X_i} w_{ij} z_j‖$$
令$Z=(z_1,z_2,…,z_m)∈R^{d×m}, (W)_{ij}=w_{ij}$,
$$M=(I-W)^T (I-W)$$
则最优化目标可重写为
$$min_Z tr(ZMZ^T), s.t.ZZ^T=I$$
利用拉格朗日乘子法可以得到$MZ=λZ$的形式，因此可对矩阵$M$进行特征值分解，取$d$个最小的非零特征值对应的特征向量组成的矩阵即为样本在低维空间的投影$Z$。算法描述如下：

输入：数据样本集${x_1,x_2,…,x_m}$，近邻参数$k$，低维空间维数$d$；
过程：
利用$k$近邻算法确定每个样本点$x_i$的邻域样本的下标集合$X_i$；
最小化重构误差计算样本$x_i$的权值系数$w_i$，并得到矩阵$M$；
对矩阵$M$进行特征值分解；
取$d$个最小的非零特征值对应的特征向量；
输出：样本集在低维空间的投影$Z=(z_1,z_2,…,z_m)$。

t分布随机邻域嵌入(t-SNE)

t-SNE是一种非线性降维方法，非常适用于高维数据降到二维或者三维空间，进行可视化。其基本原理是在高维空间中构建一个样本之间的概率分布，使得相似的样本有更高的概率被选择，而不相似的样本被选择的概率较低；然后在低维空间中构建这些样本点的概率分布，使得这两个概率分布尽可能的相似，并利用KL散度(Kullback–Leibler divergence)来度量两个分布之间的相似性。
给定一个高维空间的数据样本集${x_1,x_2,…,x_N },x_i∈R^D$，$N$为样本集的大小。假设高维空间中的任意两个样本点，$x_j$的取值服从以$x_i$为中心、$σ_i$为方差的高斯分布，同样$x_i$也服从以$x_j$为中心、$σ_j$为方差的高斯分布，这样样本点$x_j$与$x_i$相似的条件概率为
$$p_{j|i}=\dfrac{-exp(\left|x_i-x_j\right|^2 / 2\sigma^2)}{\Sigma_{k\neq i} exp(\left|x_i-x_k\right|^2 / 2\sigma^2)}$$
即$x_j$在$x_i$高斯分布下的概率占全部样本在$x_i$高斯分布下概率的多少。定义两个点相似度在全部样本两两相似度的联合概率
$$p_{ij}=(p_{j|i}+p_{i|j})/2N$$
t-SNE的目标是学习一个高维到低维的映射${y_1,y_2,…,y_N },y_i∈R^d$，在低维空间中，两个点相似度也利用联合概率来表示，假设低维空间中两点间的欧氏距离服从学生分布，两个点$y_i$和$y_j$的相似度可定义为
$$q_{ij}=\dfrac{(1+\left|y_i-y_j\right|^2)^{-1}}{\Sigma_{k\neq i} (1+\left|y_k-y_l\right|^2)^{-1}}$$
如果在高维空间中样本点之间的相似度$p_{ij}$和在低维空间中样本点之间的相似度$q_{ij}$相同，就说明低维空间的点能正确反映高维空间中的相对位置关系。t-SNE的目标就是要找到一组降维表示能够最小化$p_{ij}$和$q_{ij}$的差值，因此采用KL散度来构建目标函数
$$C=\Sigma_i KL(P_i||Q_i)=\Sigma_i \Sigma_j p_{j|i}log{\dfrac{p_{j|i}}{q_{j|i}}}$$
KL散度能够衡量两个概率分布的差别，通过梯度下降法来求输入数据对应的低维表达$y_i$。即用目标函数对$y_i$求导，梯度值为
$$\dfrac{dC}{dy_i}=4\Sigma_j(p_{ij}-q_{ij})(y_i-y_j)(1+\left|y_i-y_j\right|^2)^{-1}$$
然后更新迭代$y_i$，算法流程大致如下：

输入：数据样本集${x_1,x_2,…,x_N},x_i∈R^D$，代价函数的参数$Perp$，迭代次数$T$，学习率$η$，$momentum$项系数$α(t)$
过程：
计算给定$Perp$下的条件概率$p_{j|i}$；
分别计算高维空间样本点的相似度$p_{ij}$和低维空间样本点的相似度$q_{ij}$；
对目标函数求导，计算梯度值；
迭代更新$y_i$，直至收敛或达到最大迭代次数；
输出：低维数据表示${y_1,y_2,…,y_N},y_i∈R^d$

拉普拉斯特征映射(Laplacian Eigenmaps)

拉普拉斯特征映射和局部线性嵌入(LLE)类似，也是一种基于流形学习的数据降维方法，都是从图的角度去构建数据之间的关系。其基本思想是在高维空间中相互有关系或者说相连的样本点，在降维后的低维空间中尽可能的靠近，以反映数据内在的流形结构。
Laplacian Eigenmaps通过构建相似关系图，图中每个顶点代表一个样本点，每一条边权重代表样本之间的相似程度，距离越近的点越相似，而且权值越大，以此来重构数据流形的局部结构特征。给定一个高维空间的数据样本集$X={x_1,x_2,…,x_N },x_i∈R^D$，$N$为样本集的大小，样本集在低维空间的映射为$Y={y_1,y_2,…,y_N},y_i∈R^d$，降维后的空间维数为$d$。如果两个样本点$x_i$和$x_j$很相似，那么在降维后的空间中应该尽可能接近，因此要优化的目标函数如下：
$$min\Sigma_{i,j} W_{ij} ‖y_i-y_j ‖^2 $$
式中，$W$为一权重矩阵，$W_{ij}$为度量样本点$x_i$和$x_j$相似性的权值，可通过一个热核函数来定义：
$$W_{ij}=e^{‖x_i-x_j‖^2/i}$$
根据距离远近确定权值大小，当然也可以简单地将直接相连样本点的权值设为$1$，其他为$0$。定义一个对角矩阵$D$，对角线上元素$D_{ii}$为权重矩阵$W$第$i$行元素之和，即
$$D_{ii}=\Sigma_j W_{ij}$$
令$L=D-W$，$L$为拉普拉斯矩阵，则
$$\Sigma_{i,j} W_{ij} ‖y_i-y_j‖^2 = \Sigma_i ‖y_i‖^2 D_{ii} + \Sigma_j ‖y_j‖^2 D_{jj} - 2\Sigma_{i,j} y_i^T y_j W_{ij} = 2Y^T LY$$
因此最优化目标可重写为
$$min⁡ tr(Y^T LY), s.t.Y^T DY=I$$
使用拉格朗日乘子法，可得
$$LY=λDY$$
基于上式进行特征值分解，取$d$个最小的非零特征值所对应的特征向量组成的矩阵即为降维后的结果输出。算法流程如下：

输入：高维数据样本集$X={x_1,x_2,…,x_N},x_i∈R^D$，降维后的空间维数为$d$；
过程：
利用某种方法将所有样本点构建成一个图，例如K近邻算法，将每个点和最近的$K$个点相连；
确定点与点之间连接边的权重$W_{ij}$，例如热核函数；
进行特征映射，计算拉普拉斯矩阵最小的$d$个非零特征值对应的特征向量作为输出矩阵；
输出：样本集在低维空间的映射为$Y={y_1,y_2,…,y_N},y_i∈R^d$