图像特征提取之LBP特征

发表于   |   分类于   |     |  

  局部二值模式(Local Binary Patter, LBP)是一种用来描述图像局部纹理特征的算子，LBP特征具有灰度不变性和旋转不变性等显著优点，它将图像中的各个像素与其邻域像素值进行比较，将结果保存为二进制数，并将得到的二进制比特串作为中心像素的编码值，也就是LBP特征值。LBP提供了一种衡量像素间邻域关系的特征模式，因此可以有效地提取图像的局部特征，而且由于其计算简单，可用于基于纹理分类的实时应用场景，例如目标检测、人脸识别等。

原始LBP特征

  原始的LBP算子定义于图像中$3 \times 3$的邻域窗口，取窗口内中心像素的灰度值作为阈值，将8邻域像素的灰度值与其进行比较，若邻域像素值大于中心像素值，则比较结果取值为1，否则为0。这样邻域内的8个像素点经过比较后可得到8位二进制数，将其按顺序依次排列即可得到中心像素的LBP值。LBP特征值反映了中心像素和其邻域的纹理信息。LBP的取值一共有$2^8 = 256$种，和一幅普通的灰度图像类似，因此可将LBP特征以灰度图的形式表达出来。由于LBP特征考虑的是纹理信息，而不包含颜色信息，因此彩色图需转换为灰度图。原始LBP特征的提取过程如下图所示：

origin-LBP.jpg

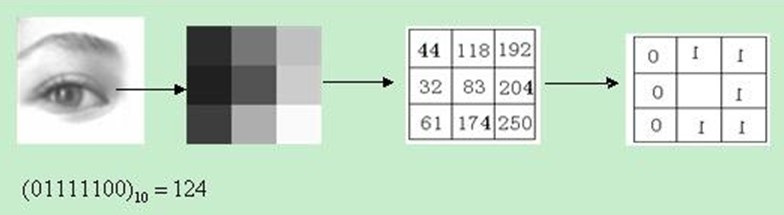
公式定义如下：
$$LBP(x_c,y_c)=\Sigma_{p=0}^{P-1} 2^p s(i_p-i_c)$$
其中$(x_c,y_c)$代表邻域窗口内的中心像素，其像素值为$i_c$，$i_p为邻域内其他像素值$，s(x)是符号函数。
原始LBP特征的实现代码(OpenCV)如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
template <typename _tp>
void getOriginLBPFeature(InputArray _src,OutputArray _dst)
{
    Mat src = _src.getMat();
    _dst.create(src.rows-2,src.cols-2,CV_8UC1);
    Mat dst = _dst.getMat();
    dst.setTo(0);
    for(int i=1;i<src.rows-1;i++)
    {
        for(int j=1;j<src.cols-1;j++)
        {
            _tp center = src.at<_tp>(i,j);
            unsigned char lbpCode = 0;
            lbpCode |= (src.at<_tp>(i-1,j-1) > center) << 7;
            lbpCode |= (src.at<_tp>(i-1,j  ) > center) << 6;
            lbpCode |= (src.at<_tp>(i-1,j+1) > center) << 5;
            lbpCode |= (src.at<_tp>(i  ,j+1) > center) << 4;
            lbpCode |= (src.at<_tp>(i+1,j+1) > center) << 3;
            lbpCode |= (src.at<_tp>(i+1,j  ) > center) << 2;
            lbpCode |= (src.at<_tp>(i+1,j-1) > center) << 1;
            lbpCode |= (src.at<_tp>(i  ,j-1) > center) << 0;
            dst.at<uchar>(i-1,j-1) = lbpCode;
        }
    }
}

圆形LBP特征(Circular LBP or Extended LBP)

  原始LBP特征考虑的是固定半径范围内的邻域像素，不能满足不同尺寸和频率纹理的需求，当图像的尺寸发生变化时，LBP特征将不能正确编码局部邻域的纹理信息。为了适应不同尺寸的纹理特征，Ojala等人对LBP算子
进行了改进，将$3 \times 3$邻域窗口扩展到任意邻域，并用圆形邻域代替了正方形邻域，改进后的LBP算子允许在半径为R的邻域内有任意多个像素点，从而得到在半径为R的区域内含有P个采样点的LBP算子。

circular-lbp.png

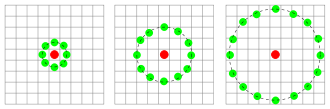
采样点的坐标可通过以下公式计算：
$$x_p=x_c+R cos(2\pi p / P)$$
$$y_p=y_c+R sin(2\pi p / P)$$
其中$(x_c,y_c)$为中心像素点，$(x_p,y_p),p\in P$为邻域内某个采样点，通过上次可以计算任意个采样点的坐标，但是得到的坐标值未必为整数，因此可通过双线性插值的方法来得到该采样点的像素值：
$$f(x, y) = \left[ \begin{matrix} 1-x& x\end{matrix} \right] \left[ \begin{matrix} f(0,0)& f(0,1)\\ f(1,0)& f(1,1)\end{matrix} \right] \left[ \begin{matrix} 1-y\\ y\end{matrix} \right]$$

圆形LBP特征的实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
//圆形LBP特征计算，这种方法适于理解，但在效率上存在问题，声明时默认neighbors=8
template <typename _tp>
void getCircularLBPFeature(InputArray _src,OutputArray _dst,int radius,int neighbors)
{
    Mat src = _src.getMat();
    //LBP特征图像的行数和列数的计算要准确
    _dst.create(src.rows-2*radius,src.cols-2*radius,CV_8UC1);
    Mat dst = _dst.getMat();
    dst.setTo(0);
    //循环处理每个像素
    for(int i=radius;i<src.rows-radius;i++)
    {
        for(int j=radius;j<src.cols-radius;j++)
        {
            //获得中心像素点的灰度值
            _tp center = src.at<_tp>(i,j);
            unsigned char lbpCode = 0;
            for(int k=0;k<neighbors;k++)
            {
                //根据公式计算第k个采样点的坐标，这个地方可以优化，不必每次都进行计算radius*cos，radius*sin
                float x = i + static_cast<float>(radius * \
                    cos(2.0 * CV_PI * k / neighbors));
                float y = j - static_cast<float>(radius * \
                    sin(2.0 * CV_PI * k / neighbors));
                //根据取整结果进行双线性插值，得到第k个采样点的灰度值
                //1.分别对x，y进行上下取整
                int x1 = static_cast<int>(floor(x));
                int x2 = static_cast<int>(ceil(x));
                int y1 = static_cast<int>(floor(y));
                int y2 = static_cast<int>(ceil(y));
                //2.计算四个点(x1,y1),(x1,y2),(x2,y1),(x2,y2)的权重
                //下面的权重计算方式有个问题，如果四个点都相等，则权重全为0，计算出来的插值为0
                //float w1 = (x2-x)*(y2-y); //(x1,y1)
                //float w2 = (x2-x)*(y-y1); //(x1,y2)
                //float w3 = (x-x1)*(y2-y); //(x2,y1)
                //float w4 = (x-x1)*(y-y1); //(x2,y2)
                //将坐标映射到0-1之间
                float tx = x - x1;
                float ty = y - y1;
                //根据0-1之间的x，y的权重计算公式计算权重
                float w1 = (1-tx) * (1-ty);
                float w2 =    tx  * (1-ty);
                float w3 = (1-tx) *    ty;
                float w4 =    tx  *    ty;
                //3.根据双线性插值公式计算第k个采样点的灰度值
                float neighbor = src.at<_tp>(x1,y1) * w1 + src.at<_tp>(x1,y2) *w2 \
                    + src.at<_tp>(x2,y1) * w3 +src.at<_tp>(x2,y2) *w4;
                //通过比较获得LBP值，并按顺序排列起来
                lbpCode |= (neighbor>center) <<(neighbors-k-1);
            }
            dst.at<uchar>(i-radius,j-radius) = lbpCode;
        }
    }
}

圆形LBP特征的效率优化版本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
//圆形LBP特征计算，效率优化版本，声明时默认neighbors=8
template <typename _tp>
void getCircularLBPFeatureOptimization(InputArray _src,OutputArray _dst,int radius,int neighbors)
{
    Mat src = _src.getMat();
    //LBP特征图像的行数和列数的计算要准确
    _dst.create(src.rows-2*radius,src.cols-2*radius,CV_8UC1);
    Mat dst = _dst.getMat();
    dst.setTo(0);
    for(int k=0;k<neighbors;k++)
    {
        //计算采样点对于中心点坐标的偏移量rx，ry
        float rx = static_cast<float>(radius * cos(2.0 * CV_PI * k / neighbors));
        float ry = -static_cast<float>(radius * sin(2.0 * CV_PI * k / neighbors));
        //为双线性插值做准备
        //对采样点偏移量分别进行上下取整
        int x1 = static_cast<int>(floor(rx));
        int x2 = static_cast<int>(ceil(rx));
        int y1 = static_cast<int>(floor(ry));
        int y2 = static_cast<int>(ceil(ry));
        //将坐标偏移量映射到0-1之间
        float tx = rx - x1;
        float ty = ry - y1;
        //根据0-1之间的x，y的权重计算公式计算权重，权重与坐标具体位置无关，与坐标间的差值有关
        float w1 = (1-tx) * (1-ty);
        float w2 =    tx  * (1-ty);
        float w3 = (1-tx) *    ty;
        float w4 =    tx  *    ty;
        //循环处理每个像素
        for(int i=radius;i<src.rows-radius;i++)
        {
            for(int j=radius;j<src.cols-radius;j++)
            {
                //获得中心像素点的灰度值
                _tp center = src.at<_tp>(i,j);
                //根据双线性插值公式计算第k个采样点的灰度值
                float neighbor = src.at<_tp>(i+x1,j+y1) * w1 + src.at<_tp>(i+x1,j+y2) *w2 \
                    + src.at<_tp>(i+x2,j+y1) * w3 +src.at<_tp>(i+x2,j+y2) *w4;
                //LBP特征图像的每个邻居的LBP值累加，累加通过与操作完成，对应的LBP值通过移位取得
                dst.at<uchar>(i-radius,j-radius) |= (neighbor>center) <<(neighbors-k-1);
            }
        }
    }
}

旋转不变LBP特征(Rotation Invariant LBP)

  无论是原始LBP算子还是圆形LBP算子，都只是灰度不变的，而不是旋转不变的，旋转图像会得到不同的LBP特征值。相关研究人员又提出了一种具有旋转不变性的LBP算子，即不断旋转圆形邻域的采样点，或者以不同的邻域像素作为起始点，顺时针遍历所有采样点，得到一系列编码值(P个)，取其中最小的作为该邻域中心像素的LBP值。旋转不变LBP算子的示意图如下：

Rota-inv-lbp.jpg

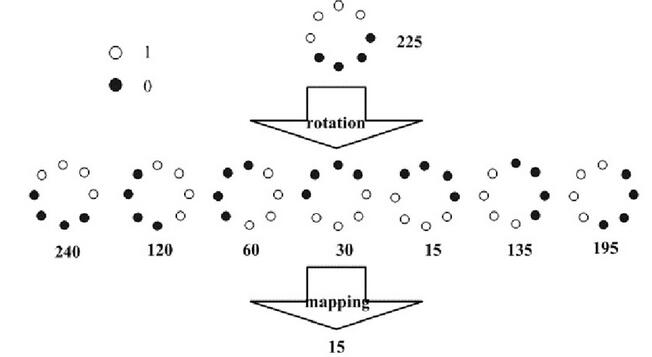
旋转不变LBP特征的实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
//旋转不变圆形LBP特征计算，声明时默认neighbors=8
template <typename _tp>
void getRotationInvariantLBPFeature(InputArray _src,OutputArray _dst,int radius,int neighbors)
{
    Mat src = _src.getMat();
    //LBP特征图像的行数和列数的计算要准确
    _dst.create(src.rows-2*radius,src.cols-2*radius,CV_8UC1);
    Mat dst = _dst.getMat();
    dst.setTo(0);
    for(int k=0;k<neighbors;k++)
    {
        //计算采样点对于中心点坐标的偏移量rx，ry
        float rx = static_cast<float>(radius * cos(2.0 * CV_PI * k / neighbors));
        float ry = -static_cast<float>(radius * sin(2.0 * CV_PI * k / neighbors));
        //为双线性插值做准备
        //对采样点偏移量分别进行上下取整
        int x1 = static_cast<int>(floor(rx));
        int x2 = static_cast<int>(ceil(rx));
        int y1 = static_cast<int>(floor(ry));
        int y2 = static_cast<int>(ceil(ry));
        //将坐标偏移量映射到0-1之间
        float tx = rx - x1;
        float ty = ry - y1;
        //根据0-1之间的x，y的权重计算公式计算权重，权重与坐标具体位置无关，与坐标间的差值有关
        float w1 = (1-tx) * (1-ty);
        float w2 =    tx  * (1-ty);
        float w3 = (1-tx) *    ty;
        float w4 =    tx  *    ty;
        //循环处理每个像素
        for(int i=radius;i<src.rows-radius;i++)
        {
            for(int j=radius;j<src.cols-radius;j++)
            {
                //获得中心像素点的灰度值
                _tp center = src.at<_tp>(i,j);
                //根据双线性插值公式计算第k个采样点的灰度值
                float neighbor = src.at<_tp>(i+x1,j+y1) * w1 + src.at<_tp>(i+x1,j+y2) *w2 \
                    + src.at<_tp>(i+x2,j+y1) * w3 +src.at<_tp>(i+x2,j+y2) *w4;
                //LBP特征图像的每个邻居的LBP值累加，累加通过与操作完成，对应的LBP值通过移位取得
                dst.at<uchar>(i-radius,j-radius) |= (neighbor>center) <<(neighbors-k-1);
            }
        }
    }
    //进行旋转不变处理
    for(int i=0;i<dst.rows;i++)
    {
        for(int j=0;j<dst.cols;j++)
        {
            unsigned char currentValue = dst.at<uchar>(i,j);
            unsigned char minValue = currentValue;
            for(int k=1;k<neighbors;k++)		//循环左移
            {
                unsigned char temp = (currentValue>>(neighbors-k)) | (currentValue<<k);
                if(temp < minValue)
                {
                    minValue = temp;
                }
            }
            dst.at<uchar>(i,j) = minValue;
        }
    }
}

LBP等价模式(Uniform LBP)

  对于一个半径为R的圆形区域，包含有P个邻域采样点，则LBP算子可能产生$2^P$种模式。随着邻域内采样点数的增加，LBP值的取值数量呈指数级增长。例如$5 \times 5$邻域内20个采样点，则对应有$2^{20}$中模式，过多的二进制模式不利于纹理信息的提取、分类、识别。例如，将LBP特征用于纹理分类或人脸识别时，一般采用LBP特征的统计直方图来表达图像的信息，而较多的模式种类将使得数据量过大，且直方图过于稀疏。因此，需要对原始的LBP特征进行降维，使得数据量减少的情况下能最好地表达图像的信息。
  为了解决二进制模式过多的问题，提高统计性，Ojala提出了一种“等价模式”(Uniform Pattern)来对LBP特征的模式种类进行降维。Ojala认为，在实际图像中，绝大数LBP模式最多只包含两次从0到1或者从1到0的跳变，“等价模式”定义为：当某个LBP所对应的循环二进制数从0到1或者从1到0最多有两次跳变时，该LBP所对应的二进制就是一个等价模式类。如00000000(0次跳变)，11000011(2次跳变)都是等价模式类。除等价模式类以外的模式都归为另一类，称为混合模式类，例如10010111(共4次跳变)。通过改进，二进制模式的种类大大减少，由原来的$2^P$中降为$P(P-1)+2+1$种，其中$P(P-1)$为2次跳变的模式数，2为0次跳变(全”0”或全”1”)的模式数，1为混合模式的数量，由于是循环二进制数，因此’0’、’1’跳变次数不可能为奇数次。对于$3 \times 3$邻域内8个采样点来说，二进制模式由原始的256种变为59种。这使得特征向量的维数大大减少，并且可以减少高频噪声带来的影响。实验表明，一般情况下，等价模式的数目占全部模式的90%以上，可以有效对数据进行降维。下图为58种等价模式类：

uniform LBP.png

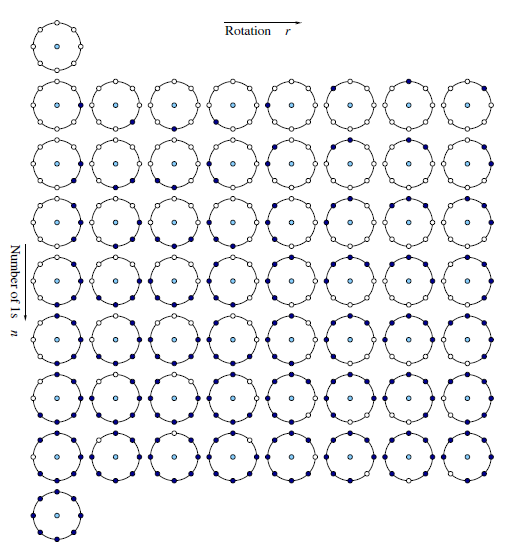
在具体实现中，等价模式类按值递增从1开始编码，混合模式类编码为0，因此得到的LBP特征图整体偏暗。LBP等价模式的实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
//等价模式LBP特征计算
template <typename _tp>
void getUniformPatternLBPFeature(InputArray _src,OutputArray _dst,int radius,int neighbors)
{
    Mat src = _src.getMat();
    //LBP特征图像的行数和列数的计算要准确
    _dst.create(src.rows-2*radius,src.cols-2*radius,CV_8UC1);
    Mat dst = _dst.getMat();
    dst.setTo(0);
    //LBP特征值对应图像灰度编码表，直接默认采样点为8位
    uchar temp = 1;
    uchar table[256] = {0};
    for(int i=0;i<256;i++)
    {
        if(getHopTimes(i)<3)
        {
            table[i] = temp;
            temp++;
        }
    }
    //是否进行UniformPattern编码的标志
    bool flag = false;
    //计算LBP特征图
    for(int k=0;k<neighbors;k++)
    {
        if(k==neighbors-1)
        {
            flag = true;
        }
        //计算采样点对于中心点坐标的偏移量rx，ry
        float rx = static_cast<float>(radius * cos(2.0 * CV_PI * k / neighbors));
        float ry = -static_cast<float>(radius * sin(2.0 * CV_PI * k / neighbors));
        //为双线性插值做准备
        //对采样点偏移量分别进行上下取整
        int x1 = static_cast<int>(floor(rx));
        int x2 = static_cast<int>(ceil(rx));
        int y1 = static_cast<int>(floor(ry));
        int y2 = static_cast<int>(ceil(ry));
        //将坐标偏移量映射到0-1之间
        float tx = rx - x1;
        float ty = ry - y1;
        //根据0-1之间的x，y的权重计算公式计算权重，权重与坐标具体位置无关，与坐标间的差值有关
        float w1 = (1-tx) * (1-ty);
        float w2 =    tx  * (1-ty);
        float w3 = (1-tx) *    ty;
        float w4 =    tx  *    ty;
        //循环处理每个像素
        for(int i=radius;i<src.rows-radius;i++)
        {
            for(int j=radius;j<src.cols-radius;j++)
            {
                //获得中心像素点的灰度值
                _tp center = src.at<_tp>(i,j);
                //根据双线性插值公式计算第k个采样点的灰度值
                float neighbor = src.at<_tp>(i+x1,j+y1) * w1 + src.at<_tp>(i+x1,j+y2) *w2 \
                    + src.at<_tp>(i+x2,j+y1) * w3 +src.at<_tp>(i+x2,j+y2) *w4;
                //LBP特征图像的每个邻居的LBP值累加，累加通过与操作完成，对应的LBP值通过移位取得
                dst.at<uchar>(i-radius,j-radius) |= (neighbor>center) <<(neighbors-k-1);
                //进行LBP特征的UniformPattern编码
                if(flag)
                {
                    dst.at<uchar>(i-radius,j-radius) = table[dst.at<uchar>(i-radius,j-radius)];
                }
            }
        }
    }
}
//计算跳变次数
int getHopTimes(int n)
{
    int count = 0;
    bitset<8> binaryCode = n;
    for(int i=0;i<8;i++)
    {
        if(binaryCode[i] != binaryCode[(i+1)%8])
        {
            count++;
        }
    }
    return count;
}

此外，旋转不变的Uniform LBP算子的等价模式类的数目为P+1个，对于8个采样点，基于等价模式的旋转不变LBP模式只有9个输出，该模式对于上图的Uniform LBP，每一行都是旋转不变的，对应同一个编码值。

多尺度LBP(Multiscale Block LBP)

  基本LBP算子获取的是单个像素和其邻域像素间的纹理信息，属于微观特征。中科院的研究人员针对此提出了一种多尺度的LBP算子，将图像分为一个个块(block)，再将每个块分为一个个的小连通区域(cell)，类似于HOG特征，cell内的灰度平均值或者和值作为当前cell的灰度阈值，与邻域cell进行比较得到LBP值，生成的特征即为MB-LBP，block大小为$3 \times 3$，cell大小为1，就是原始的LBP特征。下图所示block为$9 \times 9$，cell为$3 \times 3$。

MB-LBP.jpg

MB-LBP特征的实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//MB-LBP特征的计算
void getMultiScaleBlockLBPFeature(InputArray _src,OutputArray _dst,int scale)
{
    Mat src = _src.getMat();
    Mat dst = _dst.getMat();
    //定义并计算积分图像
    int cellSize = scale / 3;
    int offset = cellSize / 2;
    Mat cellImage(src.rows-2*offset,src.cols-2*offset,CV_8UC1);
    for(int i=offset;i<src.rows-offset;i++)
    {
        for(int j=offset;j<src.cols-offset;j++)
        {
            int temp = 0;
            for(int m=-offset;m<offset+1;m++)
            {
                for(int n=-offset;n<offset+1;n++)
                {
                    temp += src.at<uchar>(i+n,j+m);
                }
            }
            temp /= (cellSize*cellSize);
            cellImage.at<uchar>(i-cellSize/2,j-cellSize/2) = uchar(temp); 
        }
    }
    getOriginLBPFeature<uchar>(cellImage,dst);
}

多尺度模式下同样用到了降维，论文中是直接采样统计的方法对不同尺度的LBP算子的模式进行统计，选取占比例较高的模式，而不是利用跳变规则。具体来说，就是将得到的MB-LBP特征计算统计直方图，通过对bin中的数值进行排序以及权衡，将排序在前N(63)位的特征值看作是等价模式类，其余的为混合模式类，总共为N+1类，论文中称之为(SEMB-LBP, Statistically Effective MB-LBP)。
SEMB-LBP的实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
//求SEMB-LBP
void SEMB_LBPFeature(InputArray _src,OutputArray _dst,int scale)
{
    Mat dst=_dst.getMat();
    Mat MB_LBPImage;
    getMultiScaleBlockLBPFeature(_src,MB_LBPImage,scale);
    //imshow("dst",dst);
    Mat histMat;
    int histSize = 256;
    float range[] = {float(0),float(255)};
    const float* ranges = {range};
    //计算LBP特征值0-255的直方图
    calcHist(&MB_LBPImage,1,0,Mat(),histMat,1,&histSize,&ranges,true,false);
    histMat.reshape(1,1);
    vector<float> histVector(histMat.rows*histMat.cols);
    uchar table[256];
    memset(table,64,256);
    if(histMat.isContinuous())
    {
        //histVector = (int *)(histMat.data);
        //将直方图histMat变为vector向量histVector
        histVector.assign((float*)histMat.datastart,(float*)histMat.dataend);
        vector<float> histVectorCopy(histVector);
        //对histVector进行排序，即对LBP特征值的数量进行排序，降序排列
        sort(histVector.begin(),histVector.end(),greater<float>());
        for(int i=0;i<63;i++)
        {
            for(int j=0;j<histVectorCopy.size();j++)
            {
                if(histVectorCopy[j]==histVector[i])
                {
                    //得到类似于Uniform的编码表
                    table[j]=i;
                }
            }
        }
    }
    dst = MB_LBPImage;
    //根据编码表得到SEMB-LBP
    for(int i=0;i<dst.rows;i++)
    {
        for(int j=0;j<dst.cols;j++)
        {
            dst.at<uchar>(i,j) = table[dst.at<uchar>(i,j)];
        }
    }
}

图像的LBP特征向量(Local Binary Patterns Histograms)

  对图像中的每个像素求取LBP特征值可得到图像的LBP特征图谱，但一般不直接将LBP图谱作为特征向量用于分类识别，而是类似于HOG特征，采用LBP特征的统计直方图作为特征向量。将LBP特征图谱划分为若干个子连通区域，并提取每个局部块的直方图，然后将这些直方图一次连接在一起形成LBP特征的统计直方图(LBPH)，即可用于分类识别的LBP特征向量。
LBP特征向量的具体计算过程如下：

  • 按照上述算法计算图像的LBP特征图谱
  • 将LBP特征图谱分块，例如分成$8 \times 8 = 64$个区域
  • 计算每个子区域中LBP特征值的统计直方图，并进行归一化，直方图大小为$1 \times numPatterns$
  • 将所有区域的统计直方图按空间顺序依次连接，得到整幅图像的LBP特征向量，大小为$1 \times (numPatterns \times 64)$
  • 从足够数量的样本中提取LBP特征，并利用机器学习的方法进行训练得到模型，用于分类和识别等领域。

  对于LBP特征向量的维度，邻域采样点为8个，如果是原始的LBP特征，其模式数量为256，特征维数为$64 \times 256 = 16384$；如果是Uniform LBP特征，其模式数量为59，特征维数为$64 \times 59 = 3776$，使用等价模式特征，可以有效进行数据降维，而对模型性能却无较大影响。
LBP特征向量的实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
//计算LBP特征图像的直方图LBPH
Mat getLBPH(InputArray _src,int numPatterns,int grid_x,int grid_y,bool normed)
{
    Mat src = _src.getMat();
    int width = src.cols / grid_x;
    int height = src.rows / grid_y;
    //定义LBPH的行和列，grid_x*grid_y表示将图像分割成这么些块，numPatterns表示LBP值的模式种类
    Mat result = Mat::zeros(grid_x * grid_y,numPatterns,CV_32FC1);
    if(src.empty())
    {
        return result.reshape(1,1);
    }
    int resultRowIndex = 0;
    //对图像进行分割，分割成grid_x*grid_y块，grid_x，grid_y默认为8
    for(int i=0;i<grid_x;i++)
    {
        for(int j=0;j<grid_y;j++)
        {
            //图像分块
            Mat src_cell = Mat(src,Range(i*height,(i+1)*height),Range(j*width,(j+1)*width));
            //计算直方图
            Mat hist_cell = getLocalRegionLBPH(src_cell,0,(numPattern-1),true);
            //将直方图放到result中
            Mat rowResult = result.row(resultRowIndex);
            hist_cell.reshape(1,1).convertTo(rowResult,CV_32FC1);
            resultRowIndex++;
        }
    }
    return result.reshape(1,1);
}
//计算一个LBP特征图像块的直方图
Mat getLocalRegionLBPH(const Mat& src,int minValue,int maxValue,bool normed)
{
    //定义存储直方图的矩阵
    Mat result;
    //计算得到直方图bin的数目，直方图数组的大小
    int histSize = maxValue - minValue + 1;
    //定义直方图每一维的bin的变化范围
    float range[] = { static_cast<float>(minValue),static_cast<float>(maxValue + 1) };
    //定义直方图所有bin的变化范围
    const float* ranges = { range };
    //计算直方图，src是要计算直方图的图像，1是要计算直方图的图像数目，0是计算直方图所用的图像的通道序号，从0索引
    //Mat()是要用的掩模，result为输出的直方图，1为输出的直方图的维度，histSize直方图在每一维的变化范围
    //ranges，所有直方图的变化范围（起点和终点）
    calcHist(&src,1,0,Mat(),result,1,&histSize,&ranges,true,false);
    //归一化
    if(normed)
    {
        result /= (int)src.total();
    }
    //结果表示成只有1行的矩阵
    return result.reshape(1,1);
}

  除了以上几种比较经典的LBP特征外，还有诸多变种，如TLBP(中心像素与周围所有像素比较，而不是根据采样点的数目)，DLBP(编码4邻域的灰度变化，每个方向上用两个比特编码)，MLBP(将中心像素值替换为采样点像素的平均值)，VLBP，RGB-LBP等。

LBP特征的应用

目标检测

  人脸检测中比较典型的模型是Haar特征 + AdaBoost分类器，目前OpenCV也支持LBP + AdaBoost和HOG + AdaBoost的方法进行目标检测，而且LBP特征的训练速度较快，适用于实时检测场景。

人脸识别

  人脸识别中LBP特征向量主要是用于直方图的比较，通过距离度量的方式(例如方差)找到训练数据中与输入图像距离最小的特征向量，将其对应的类别作为识别结果输出。

reference