图像特征描述子之PCA-SIFT与GLOH

SIFT和SURF是两种应用较为广泛的图像特征描述子，SURF可以看做是SIFT特征的加速版本。在SIFT的基础上，又陆续诞生了其他的变体：PCA-SIFT和GLOH(Gradient Location-Orientation Histogram)。

PCA-SIFT

SIFT特征提取主要分为4步：尺度空间构建，关键点定位，主方向分配，生成特征描述子。PCA-SIFT的前3步和标准SIFT相同，也就说PCA-SIFT和标准SIFT具有相同的尺度空间、亚像素定位以及主方向。但在生成特征描述子时，使用特征点周围$41 \times 41$的邻域计算特征向量，并通过主成分分析(PCA)，对特征向量进行降维，以滤除噪声，保留有效信息，并提高匹配效率。PCA-SIFT生成特征描述子的算法流程如下：

以特征点为中心，选定$41 \times 41$的矩形邻域
计算邻域内所有像素水平和垂直方向的梯度(偏导数)，得到一个$39 \times 39 \times 2 = 3042$维的特征向量(不计最外层像素)
假设有$N$个特征点，所有特征点描述子向量构成一个$N \times 3042$的矩阵，计算所有向量的协方差矩阵$C$
计算协方差矩阵$C$前$k$个最大特征值对应的特征向量，组成一个$3042 \times k$的投影矩阵$T$
对于新的特征描述子向量，乘以投影矩阵$T$，可以得到降维后的特征向量

实际上，第3步和第4步一般提前计算好，也就是投影矩阵$T$是事先通过大量典型样本的训练得到。关于维数$k$的选择，可以是一个经验设定的固定值，也可以是基于特征值能量百分比动态选择。一般取20可得到较佳的效果。
PCA-SIFT描述子和标准SIFT相比，在保持各种不变性的同时，降低了特征向量的维数，使得特征点匹配速度大大提升。但其缺点是事先需要有一组典型图像的学习，而且，训练得到的投影矩阵只适用于同类的输入图像。

GLOH

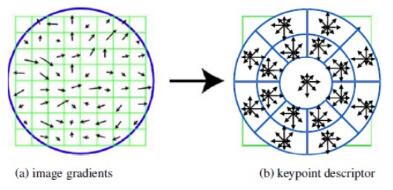
梯度位置方向直方图(Gradient Location-Orientation Histogram, GLOH)也是SIFT特征描述子的一种扩展，其目的是为了增加特征描述子的鲁棒性和独特性。GLOH把标准SIFT中$4 \times 4$的邻域子块改成仿射状的对数-极坐标同心圆，同心圆半径分别设为6、11、15。在角度方向分成8等分，每等分为$\pi / 4$，这样一共产生了17个图像子块。如下图所示，在每个子块中，计算梯度方向直方图，梯度方向分为16个方向区间，因此可生成一个$17 \times 16 = 272$的特征向量。借助PCA-SIFT的思想，通过事先建立典型图像的协方差矩阵，并得到投影矩阵。然后，对每个特征点进行PCA降维处理，最终得到一个128维的特征向量，与标准SIFT保持一致。此外，也可以对GLOH进行简化，在生成梯度直方图时，只分8个方向，这样特征向量的维数为$17 \times 8 = 136$，就不需要进行降维处理，减少对样本图像的依赖性。

result

SIFT、PCA-SIFT、GLOH的实验结果如下所示

PCA-SIFT

GLOH

result

reference