Deep Learning -- Activation Function

神经网络的激活函数(activation function)通过引入非线性因素，使得网络可以逼近任何非线性函数，提高网络模型的表达能力，更好地解决复杂问题。

Overview

激活函数通常具有以下性质：

非线性：使用非线性激活函数的多层神经网络可以逼近所有函数
可微性：对于常见的优化方法——梯度下降法，可微性是必要的
单调性：单调激活函数能够保证单层网络是凸函数
输出范围：激活函数输出值是有限的时候，基于梯度的优化方法会更加稳定，因为特征的表示受有限权值的影响更显著；当输出值的范围无界时，模型训练会更加高效，不过这种情况下一般需要更小的学习率(learning rate)，以保证收敛

Sigmoid

Sigmoid的数学公式为$f(x)=\dfrac{1}{1+e^{-x}}$，将输入映射到区间(0, 1)，函数曲线如下图所示:

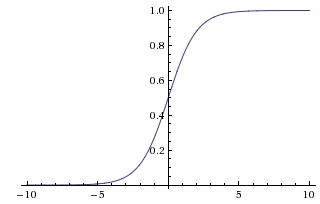
Sigmoid函数曾被广泛使用，但现在使用较少，主要是存在以下缺点：

函数饱和造成梯度消失(Sigmoids saturate and kill gradients)：神经元的激活值在趋近0或1时会饱和，在这些区域梯度值几乎为0，而且梯度值非0的输入范围非常有限。在反向传播时，此处局部梯度值将与损失函数关于该神经元输出的梯度相乘，如果局部梯度非常小，那么相乘的结果也会趋近于0，造成梯度消失，使得前面网络的权值参数无法更新。为了防止饱和，初始化权重不易过大，否则大多数神经元将会饱和，导致网络难以学习。
Sigmoid输出不是0均值(Sigmoid outputs are not zero-centered)：这一性质会导致后面网络层得到的输入数据不是零中心的，影响梯度下降的运作。因为如果输入神经元的数据总是正数（比如在$f=w^T x + b$中每个元素都$x>0$），那么关于$w$的梯度在反向传播的过程中，要么全部是正数，要么全部是负数（具体依整个表达式$f$而定）。这将会导致梯度下降权重更新时出现z字型的下降。然而，如果是按batch去训练，那么每个batch可能得到不同的信号，整个批量的梯度加起来后，对于权重的最终更新将会有不同的正负，在一定程度上减轻了这个问题。

此外，Sigmoid函数涉及到指数运算，增加了计算量。

tanh

双曲正切函数的数学表达式为$f(x)=\dfrac{1-e^{-2x}}{1+e^{-2x}}=2Sigmoid(2x)-1$，函数曲线如下图所示，输出值的范围为(-1, 1)

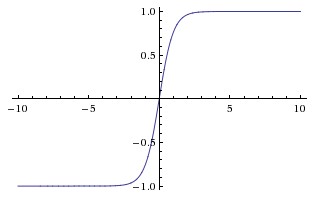
tanh函数同样存在饱和和梯度消失问题，但输出是0均值的，因此在一定程度上，性能略优于Sigmoid。

Rectified Linear Units(ReLU)

ReLU应用较为广泛，其数学表达式为$f(x)=max(0,x)$，函数曲线如左下图所示

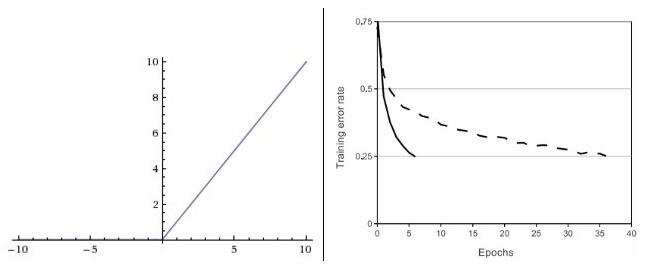
ReLU激活函数主要有如下优缺点：

(+)相比于Sigmoid和tanh，ReLU对于随机梯度下降(SGD)的收敛有显著的加速作用（在AlexNet中，比tanh收敛快6倍）。据称这是由其(分段)线性、非饱和导致的
(+)Sigmoid、tanh包含指数运算，耗费计算资源，而ReLU通过和阈值比较即可得到激活值，不涉及复杂运算
(-)ReLU的缺点是在训练时神经元比较脆弱，可能会“死掉”。当一个很大的梯度反向传播经过ReLU神经元时，可能会导致权值更新过后，对任何数据都不再出现激活现象，所有流过该神经元的梯度都将变为0。也就是说，ReLU单元在训练中将不可逆转的死亡，导致数据多样性的丢失。实际上，如果学习率设置得过高，网络中约40%的神经元都会死掉，在整个训练集中都不会再激活。因此需要合理设置学习率。

$w$是二维时，ReLU的效果如图：

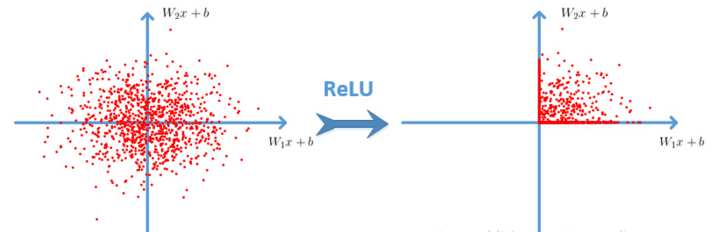
leaky-ReLU、P-ReLU、R-ReLU、ELU

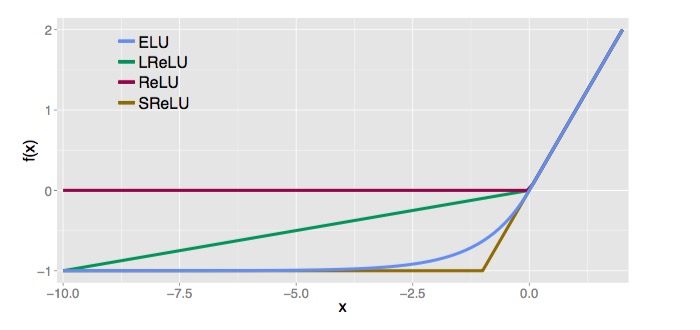
leaky-ReLU是用于解决ReLU中神经元死亡的尝试方案，其数学公式如下：
$$f(x)=\begin{cases} \alpha x, x<0 \\ x, x \geq 0 \end{cases}$$
$\alpha$是一个很小的常数，可取值为0.01。有研究论文指出，leaky-ReLU激活函数的效果不错，但不是很稳定。Kaiming He等人在2015年发布的论文Delving Deep into Rectifiers中介绍了一种新方法Parametric ReLU，把负区间上的斜率$\alpha$当做每个神经元中的一个参数来训练，然而该激活函数在在不同任务中表现的效果也没有特别清晰。在另外一个版本Randomized ReLU中

$$y_{ji}=\begin{cases} a_{ji}x_{ji}, x_{ji}<0 \\ x_{ji}, x_{ji} \geq 0 \end{cases}$$

在训练过程中，$a_{ji}$是从一个高斯分布$U(l,u)$中随机选取的；在测试阶段是固定的，将训练过程中的所有$a_{ji}$取平均值，测试阶段激活函数为$y_{ji}=\dfrac{x_{ji}}{(l+u)/2}$。此外，还有一个ELU版本，公式定义如下(式中$a>0$)，相关内容可参考文献ELU
$$f(x)=\begin{cases} a(e^x-1), x<0 \\ x, x \geq 0 \end{cases}$$

Maxout

Maxout源于大神Goodfellow在2013年发表的一篇论文Maxout Network，可以将其看作网络中的激活函数层。假设网络某一层的输入特征向量为$x=(x_1,x_2,…,x_d) \in R^d$，Maxout隐层神经元的计算公式如下：
$$h_j(x)=max_{j \in [1,k]} z_{ij}$$
$$z_{ij}=x^TW_{…ij}+b_{ij}$$
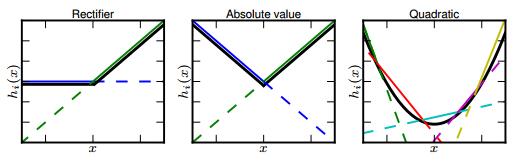
式中，$W \in R^{d \times m \times k},b \in R^{m \times k}$，是需要学习的参数，$k$是Maxout层所需要的参数。对于传统的MLP算法，从第$l$层到第$l+1$层的某个神经元，其输入为$x_i ^{(l+1)} = w_i ^{(l+1)} y^{(l)}+b_i ^{l+1}$，对第$l$层每个神经元，原本只需要学习一组参数，引入了Maxout后，需要训练$k$组，并从中选取最大的输入值作为该神经元的激活值，相当于激活函数是一个分段线性函数。因此，Maxout可以说是ReLU和Leaky-ReLU的一般化归纳。Maxout具备ReLU的优点（线性、非饱和），而没有其缺点（神经元死亡）。Maxout在MLP网络和卷积网络中均可以使用，而且其参数是可学习的，激活函数并不固定。Maxout的本质就是一个线性分段函数，可以拟合任意的凸函数（“隐隐含层”节点数k足够大时），如下图所示。和其他激活函数相比，Maxout存在参数激增的现象(k倍)。

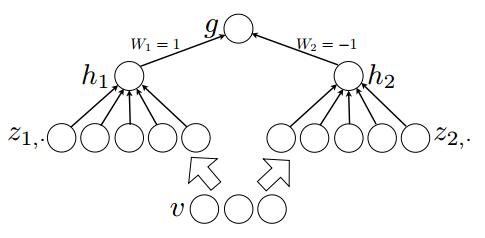
论文中给出了相关定理：对于任意的一个连续分段线性函数$g(v)$，可以找到两个凸的分段线性函数$h1(v)、h2(v)$，使得这两个凸函数的差值为$g(v)$。

Summary

通常来说，在一个网络中很少使用多种激活函数。如果使用ReLU，需要合理设置学习率，避免出现过多死亡神经元，也可以使用leaky-ReLU或者Maxout来解决该问题。