Deep Learning -- Dropout

训练神经网络模型时(Nerual Network)，如果网络规模较大，训练样本较少，为了防止模型过拟合，通常会采用Regularization(正则化，e.g. L2-norm、Dropout)。Dropout的基本思想是在模型训练时，让某些神经元以一定的概率不工作。

Overview

深度学习领域大神Hinton在2012的一篇文献《Improving neural networks by preventing co-adaptation of feature detectors》中提出，在每次训练的时候，让一半的特征检测器停止工作，可以提高网络模型的泛化能力。Hinton认为过拟合可通过阻止某些特征的协同作用来缓解，并将这种方法称之为Dropout。
Dropout的工作原理是在模型的迭代训练过程中，让网络中的某些隐层节点(神经元)以一定概率不工作，相当于去除部分节点，但节点的权重会保留下来，只是暂时不更新。每次迭代去除的节点不一样，这样相当于每次训练不同的网络，而且实现了网络的权值共享。

Procedure

在训练一个普通的多层神经网络时，其流程是：将输入样本通过网络前向传播计算每次的激活值，并得到最后的Loss Function，然后反向传播误差并更新每层的权值参数。使用Dropout后，网络模型变化如下图所示：

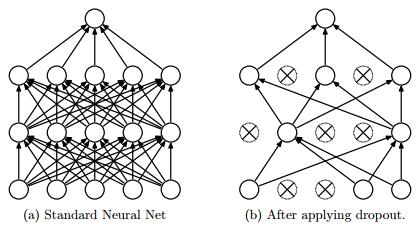
如何实现让神经元以一定概率停止工作，可参考以下公式，一般情况下，网络的前向计算公式如下：

$$z_i ^{(l+1)} = w_i ^{(l+1)} y^{(l)} + b_i ^{(l+1)}$$
$$y_i ^{(l+1)} = f(z_i ^{(l+1)})$$
采用Dropout后计算公式变成：
$$r_j ^{(l)} \sim Bernoulli(p), \overline{y}^{(l)} = r^{(l)} \ast y^{(l)}$$
$$z_i ^{(l+1)} = w_i ^{(l+1)} \overline{y}^{(l)} + b_i ^{(l+1)}, y_i ^{(l+1)} = f(z_i ^{(l+1)})$$
上式中，$r_j ^{(l)}$服从概率为$p$的伯努利二项分布，$r^{(l)}$为生成的0、1向量。通过将激活值置0，实现了网络中$l$层部分节点停止工作，而$l+1$层的输入中，也只考虑了$l$层中非0的节点（其实考虑了所有节点，只是输出为0的结点对下一层网络不起作用，在反向传播时，也无法更新和其相关的网络权值）。关于Dropout还有几点需要注意：

如果网络某一层的神经元个数为1000，dropout的比例为0.4(p=0.6)，那么经过Dropout操作后，大约会有400个神经元的激活值会置0
每次训练迭代，都会重新随机选取一定比例的节点激活值置0，因此每次删除的节点会有差异
反向传播时，非0节点的权值参数得到更新，而0节点的权值保持不变
删除某些节点使其激活值为0后，需要对其他节点进行rescale，也就是乘以$1/p$(p是保留节点的比例)；如果训练时没有rescale，测试时则需要对权重rescale，$W_{test}=pW$

Explanation

关于Dropout能够缓解过拟合、提高模型泛化能力的几点直观解释：

减少神经元之间的共适应关系：在迭代训练时，隐层节点以一定概率随机出现(或消失)，因此不能保证每两个节点同时出现，这样权值的更新不再依赖于有固定关系的隐层节点，阻止了某些特征在其他特征下才有效果的情况，迫使网络学习更鲁棒的特征
模型平均作用：Dropout删除不同的神经元，类似于每次训练不同的网络，整个训练过程相当于对不同的模型取平均，而且不同的网络结构共享权值参数

Summary

Dropout比较适用于大型网络缓解过拟合，能够取得明显的效果，但网络的训练速度也会明显变慢，不过对测试没有影响。

Overview

Procedure

Explanation

Summary

reference