Deep Learning -- Regularization

在训练神经网络时，为了缓解网络规模较大、训练数据较少而可能导致的过拟合(Overfitting)问题，通常会采取正则化(Regularization)方法，以提高模型的泛化能力。

Overview

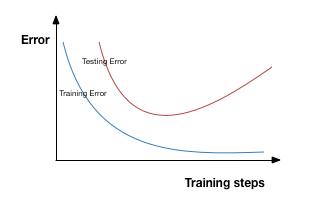
过拟合具体表现如下图所示，在迭代训练的过程中，模型复杂度增加，在训练集上的错误率降低，而在验证集上反而上升，也就是说，模型过拟合了训练集，在除训练集以外的其他数据集上表现较差。有较多的方法可用来缓解过拟合问题，例如减小网络规模，扩增数据集(Date Argumentation)、正则化(Regulariztion)、提前终止(Early stopping)等。由于较大的网络规模通常具有较强的模型表达能力，所以减小网络规模以缓解过拟合并不十分可取。正则化则是一种使用较为广泛的方法，主要有L1-norm、L2-norm、Dropout。

L2 Regularization

L2正则也称为权重衰减(Weights Decay)，直接在代价函数(Loss Function)后面增加一个L2范数的正则化项，也就是对网络中所有权值求平方和。数学表达式如下：
$$C = C_0 + \dfrac{\lambda}{2n} \Sigma_w w^2$$
式中，$C_0$为原始代价函数，$n$为训练集大小，$\lambda$是两项的平衡系数。L2正则项通过惩罚(penalizes)权重的平方，倾向于让网络学习到更小的权值。添加正则项后的代价函数对网络参数的梯度为
$$\dfrac{\partial C}{\partial w} = \dfrac{\partial C_0}{\partial w} + \dfrac{\lambda}{n}w, \dfrac{\partial C}{\partial b} = \dfrac{\partial C_0}{\partial b}$$
梯度反向传播用于更新网络权值
$$w = w - \eta (\dfrac{\partial C_0}{\partial w} + \dfrac{\lambda}{n}w) = (1-\dfrac{\eta \lambda}{n})w - \eta \dfrac{\partial C_0}{\partial w}$$
$$b = b - \eta \dfrac{\partial C_0}{\partial b}$$
式中，$\eta$为学习率(learning rate)，$w$的系数$(1-\dfrac{\eta \lambda}{n})$使得权重相比未正则化时减小，这也是$L2-norm$称作权重衰减的原因。
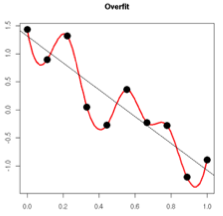
更小的权重，如何保证能够缓解过拟合？从某种意义上，权重越小表示模型复杂度更低，对数据的拟合刚好。在实际应用中，也验证了L2正则化的效果往往更好。过拟合的时候，拟合函数的系数通常较大，如下图所示，拟合函数需要顾及每个数据点，因此波动较大。在一些较小的区间内，函数值变化剧烈，意味着函数在这些小区间内的导数值（绝对值）非常大。由于自变量值可大可小，所以只有系数足够大，才能保证导数值很大。而L2正则化通过约束权值参数的范数使其不要太大，可以在一定程度上减少过拟合情况。

L1 Regularization

L1正则是在原始的代价函数后增加一个L1范数的正则化项，即所有权重绝对值的和。数学表达式如下：
$$C = C_0 + \dfrac{\lambda}{n} \Sigma_w ||w||_1$$
梯度计算公式为
$$\dfrac{\partial C}{\partial w} = \dfrac{\partial C_0}{\partial w} + \dfrac{\lambda}{n}sgn(w)$$
式中$sgn(w)$表示权重的符号，权重更新规则为
$$w = w - \eta (\dfrac{\partial C_0}{\partial w} + \dfrac{\lambda}{n}sgn(w))$$
L1正则化对梯度的影响不再与权重$w$线性相关，而是一个常量因子。当$w$为正时，更新后的$w$变小；当$w$为负时，更新后的$w$变大。因此L1正则化的效果就是让$w$往0靠，使网络中的权重尽可能为0，也就相当于减小了网络复杂度，防止过拟合。与L2-norm相比，L1-norm会导致参数稀疏，因此可用于特征选取，参数被惩罚为0的特征可以被丢弃。

Dropout

L1、L2正则化是通过修改代价函数来实现的，而Dropout则是修改神经网络本身，使得网络中的部分神经元以一定概率停止工作，具体内容可参考博文Dropout

Data Argumentation

引起过拟合的一个因素就是数据量较少，扩增数据集，可以适应更深的网络模型，训练表达能力更强的模型。数据扩增的方法主要有：

沿水平方向将图像左右翻转
平移、缩放、旋转或者随机裁剪图像
添加随机噪声

Early Stopping

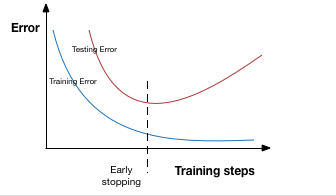
过拟合在验证集上表现为模型的错误率降到最低后上升，因此提前终止就是在模型的错误率降到最低，性能变坏之前停止迭代训练，如下图所示。当然在实际训练过程中，并不需要如此操作，而且通过设置checkpoints，每迭代一定次数保存模型，最后选择最优的作为最终模型。

关于数据集的划分：
一般数据集分为三部分：训练集(training data)、验证集(validation data)、测试集(testing data)。训练集用于在迭代训练中计算梯度、更新网络权值。验证集则在训练中评估模型的性能，用于确定一组模型的超参数，如学习率等；也就是说通过验证集，需要确定一组最优的超参数，以及在该组超参数下训练出的网络模型。而测试集则用于评估最终的模型性能，既不参与训练，也不用于选取超参数。验证集和测试集容易搞混，如果直接将测试集作为验证集使用，随着训练的进行，网络实际上在拟合测试集中的数据，那么测试集对网络的评估没有任意意义，因为最终用于评估模型的数据集应当是一个未知数据集，不参与任何训练过程。