Deep Learning -- Normalization

Normalization可理解为归一化、标准化或者规范化，广泛应用于诸多领域。整体来讲，Normalization扮演着对数据分布重新调整的角色。在图像处理领域，不同形式的归一化可以改变图像的灰度、对比度信息；在机器学习和神经网络中，Normalization可用于对数据去相关，加速模型训练，提高模型的泛化能力。

Normalization(min-max)

通常意义上的归一化，也是使用较为频繁的一种是对数据按比例缩放，使之分布在一个特定的区间。例如将数据映射到[0, 1]区间，这在数据挖掘和机器学习中较为常见，在原始数据集中，不同维的数据（特征）往往具有不同的量纲或范围，会导致不同特征呈现不同的重要性，为了消除这种影响，将不同维的特征归一化到特定区间，使所有指标处于同一数量级，将归一化的数据应用于后续的算法模型，也会更加高效便捷。归一化的数学表达式如下：
$$x = \dfrac{x-x_{min}}{x_{max}-x_{min}}$$
如果是映射到特定区间[a,b]，公式如下：
$$x = \dfrac{x-x_{min}}{x_{max}-x_{min}} (b-a) + a$$
在图像处理中，经常会将像素灰度值映射到区间[0,255]。此外，还有直方图均衡化(Histogram Equalization)、按特定幂函数对图像进行对比度拉伸(Contrast Stretching)等图像预处理操作。

Standardization

z-score标准化方法使数据符合均值为0、标准差为1的分布，数学变换式如下：
$$\widehat x = \dfrac{x - \mu}{\sigma}$$
式中，$\mu、\sigma$分别为原始数据的均值和标准差。这种标准化方法在一定程度上可以降低数据之间的相关性，并加速训练过程。就图像和视觉领域而言，通常只需要减去均值即可。对于所有图像样本，对相同坐标的像素求取均值，这样便可得到一个均值模板图像，然后让所有图像减去这个均值模板，这是一种比较通用的处理方法；还有一种是对所有图像的所有像素在RGB三个通道求取均值，然后让所有像素的三通道值分别减去对应通道的均值，这种方法有在Faster R-CNN等系列目标检测领域中用到。

ZCA Whitening

白化(Whitening)的目的是降低数据之间的相关性，对于图像数据而言，相邻像素之间具有很强的相关性，也就是说数据是冗余的。通过白化过程，希望数据具备如下两点性质：

特征之间的相关性降低
所有特征具有相同的方差

主成分分析(PCA)一般用于数据降维，其思路是计算数据样本集$X$协方差矩阵的特征值和特征向量，通过选取前k个特征值对应的特征向量组成投影矩阵，将原始数据映射到新的特征空间，这样便去除了数据之间的相关性（具体内容可参考博文）。白化的第一步操作就是PCA，如下图所示，假设由特征向量组成的变换矩阵为$U$（既可以保留所有特征向量，也可以只取前k个），那么变换后的数据为
$$X_{PCA}=U^T X$$

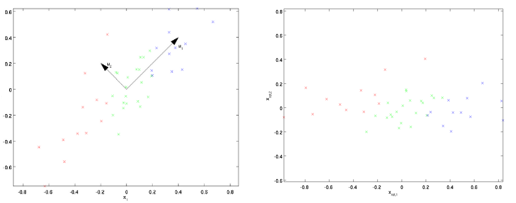
第二步PCA白化对变换后数据的每一维特征做标准差归一化处理，使得不同特征的方差相同（单位方差），变换式如下：
$$X_{PCAwhite} = \dfrac{X_{PCA}}{std(X_{PCA})}$$
也可直接采用下式：
$$X_{PCAwhite} = \dfrac{X_{PCA}}{\sqrt{\lambda_i + \varepsilon}}$$
$\lambda_i$是PCA得到的特征值，$\varepsilon$是正则化项，避免除数为0，一般取值为$\varepsilon \approx 10^{-5}$。PCA白化后数据分布如下图所示：

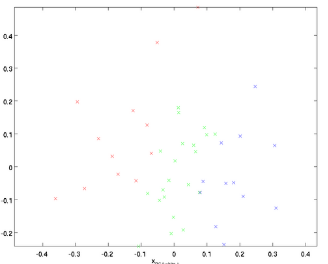
第三步ZCA白化是在PCA白化的基础上，将数据变换回原来的特征空间，使得白化后的数据尽可能地接近原始数据。
$$X_{ZCAwhite} = U X_{PCAwhite}$$

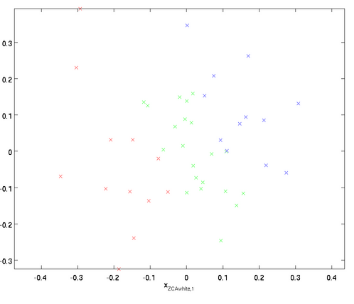
不同于 PCA白化，当使用ZCA白化时，通常保留数据的全部n个维度，不尝试去降低它的维数。关于图像的协方差矩阵和ZCA白化可参考Learning Multiple Layers of Features from Tiny Images

Global Contrast Normalization(GCN)

全局对比度标准化(GCN)就是计算图像中所有像素的均值和标准差，然后每个像素分别减去权值并除以标准差，GCN和ZCA Whitening通常一起使用。

Local Contrast Normalization(LCN)

局部对比度标准化(LCN)是通过计算图像中局部邻域的均值和标准差来进行标准化，可参考论文What is the Best Multi-Stage Architecture for Object Recognition，具体流程如下：

对图像中的像素，考虑一个$3 \times 3$的邻域
计算邻域窗口内所有像素的均值(mean)和标准差(std)，并让中心像素减去均值
比较标准差与1的大小，如果大于1，则中心像素值（减去均值后）除以标准差作为标准化后的最终值；否则，直接将减去均值后的中心像素值作为最终值
遍历图像中的所有像素，按照上述流程分别进行局部标准化

在实际处理过程中，可以考虑不同窗口大小的邻域，也可利用加权的方式求取邻域像素的均值。如果在卷积神经网络中，存在多个特征图(feature map)的情况，可以同时考虑空间邻域和特征邻域，例如相邻两个特征图的$3 \times 3$邻域，则每个像素有$3 \times 3 \times 3 -1 = 26$个邻域像素点。LCN可以增强某些特征图的特征表达能力，而限制另外一些特征图的特征表达(?)。

Local Response Normalization(LRN)

局部响应标准化(LRN)这一概念是在AlexNet中提出的，受到LCN的启发，通过考虑相邻特征图进行标准化，数学表达式如下：
$$b_{x,y}^i = a_{x,y}^i / (k + \alpha \Sigma_{j=max(0,i-n/2)}^{min(N-1, i+n/2)}(a_{x,y}^j)^2)^\beta$$
$a_{x,y}^i$是第$i$个卷积核在特征图中坐标$(x,y)$处的激活输出，$b_{x,y}^i$为对应的LRN输出值，$N$是卷积核或者特征图的数量，$n$是考虑的邻域特征图个数，论文中取值为5，$k、\alpha、\beta$是超参数，分别取值为$k=2,\alpha=10^{-4},\beta=0,75$。LRN的流程图如下：

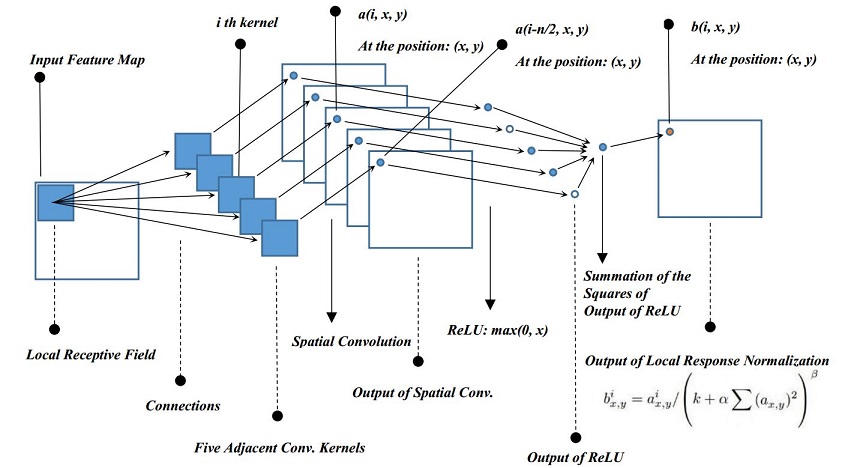
为了使LRN输入输出的特征图数量一致，需要对特征图进行扩充(padding)，两端分别增加$n/2$个特征图，可直接拷贝相邻特征图。后续有研究表明，LRN在实际模型中发挥的作用不大，因而使用逐渐变少。

Batch Normalization

在训练神经网络模型时，由于网络参数在不断更新，每一层的输入分布也在不断变化，这迫使网络设置更小的学习率，导致更慢的训练速度，而且对参数初始化的要求也较高，这种现象称为Internal Convariate Shift。而Batch Normalization通过对每层的输入进行归一化，可以有效地缓解这个问题，网络可以使用较大的学习率，参数初值也无需刻意设置，并且可以起到正则化(Regularization)的作用，减弱了对Dropout的需求，保证了更快的训练速度和更精确的网络模型。

Internal Convariate Shift

在统计机器学习中，一个经典假设就是源空间和目标空间的数据分布是一致的，如果不一致，则引入了新的研究分支，如Transform Learning、Domain Adaptation。而covariate shift就是数据分布不一致的一个子问题，表示源空间和目标空间的条件概率是一致的，但是其边缘概率不同，即对所有的$x \in \mathcal{X},P_s(Y|X=x)=P_t(Y|X=x)$，但是$P_s(X) \neq P_t(X)$。对于神经网络的各层输出，由于它们经过了层内操作作用，其分布显然与各层对应的输入分布不同，而且差异会随着网络深度增大而增大，可是它们对应的样本标记（label）仍然是不变的，这便符合了covariate shift的定义。由于是对层间信号的分析，也即是“internal”的来由。

Why need BN

在神经网络中，最基本的参数优化方法就是随机梯度下降(SGD)，通过最小化代价函数来求得一组模型参数
$$\theta = \underset{\theta}{\mathrm{arg min}} \dfrac{1}{N} \sum_{i=1}^N{\mathcal L\left(x_i, \theta\right)}$$
在实际训练过程中，通常采用minibatch的方法，即每次迭代训练一批数据，梯度计算如下：
$$\dfrac{1}{m}\sum \dfrac{\partial{\mathcal L \left(x_i, \theta\right)}}{\partial \theta}$$
minibatch可以近似整个训练集的梯度，并且可以并行地计算m个样本，比单独计算每个样本要快。但SGD仍然存在一些固有缺陷：

学习率比较难设置，为了尽量避免梯度弥散(Gradiant Vanish)，只能设置较小的学习率，导致训练缓慢
对权值参数的初始值要求较高，否则会造成收敛困难
每层的输入受到前面参数的影响，前面很小的变动，随着网络层数增加会不断被放大

参数的更新会导致各层输入数据分布的变化，每次迭代，网络中的每一层需要学习拟合不同的数据分布，这样会显著降低网络的训练速度。当一个学习系统的输入分布是变化的，例如训练集和测试集的样本分布不一致，训练的模型就很难有较好的泛化能力。通常在将原始数据输入到网络中训练时，都会有一个归一化的预处理，也就是使得数据分布的均值为0、方差为1的近似白化过程。而Batch Normalization正是将这种归一化的方法应用到网络的每一层中，这样每一层的输入分布都不再受到前面参数变化的影响，该层网络也不需要适应输入分布的变化。

考虑到网络使用饱和非线性的激活函数例如Sigmoid，参数的变化可能会导致输入大量分布于饱和区域，局部梯度趋近于0，在反向传播的时候可能会出现梯度弥散的情况，进一步导致前面参数更新较慢或者停止更新，模型收敛困难。ReLU激活函数、合适的初值以及较小的学习率可以在一定程度上解决梯度消失的问题，而采用Batch Normalization的方法使每一层的输入分布更稳定，哪怕是使用Sigmoid激活函数，输入也不太可能分布于饱和区域，降低了模型对激活函数选择的依赖。

在传统的深度网络中，过高的学习率会导致梯度爆炸或消失(explode or vanish)，以及陷入局部极值，BN可以防止参数变化的影响逐层放大，避免陷入饱和区域。而且BN使得训练对参数的尺度(scale)更加鲁棒，一般高学习率会增加参数的scale，在反向传播中放大梯度，导致模型爆炸。在进行BN之后，
$$BN(wu) = BN((\alpha w)u)$$
$$\frac{\partial BN((\alpha w)u)}{\partial u} = \frac{\partial BN(wu)}{\partial u}$$
$$\frac{\partial BN((\alpha w)u)}{\partial (\alpha w)} = \frac{1}{\alpha} \frac{\partial BN(wu)}{\partial w}$$
可以看出较大的$w$将获得较小的梯度，也就是说较大的权值更新较小，较小的权值更新较大。因此，BN使得权重的更新更加稳健，反向传播的梯度不受参数scale的影响，解决了梯度爆炸或梯度消失的问题。

What is BN

Batch Normalization作用在每一层的输入，也就是激活函数（非线性变换）之前，而不是前一层的输出，BN的算法流程如下：

BN Transform在对输入数据做0均值、单位方差的归一化处理后，又进行了一次线性变换，引入了一对可学习的参数$\gamma、\beta$，提升了模型的容纳能力(capacity)，如果$\gamma=\sqrt{\sigma_{\beta}^2}、\beta=\mu_{\beta}$，这样$y_i$就恢复成原来的输入分布$x_i$。至于是否需要对$y_i$进行还原，则由网络模型自动从训练数据中学习决定。BN层的梯度反向传播公式如下：

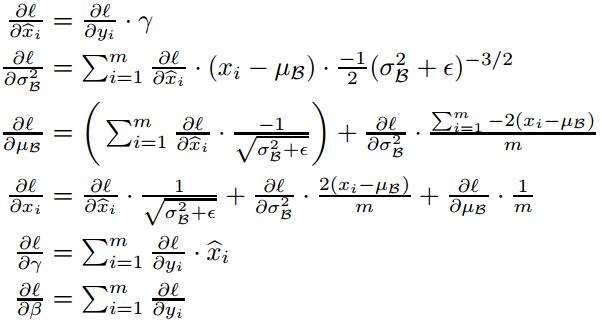
训练结束将模型用于测试时，均值$\mu$和标准差$\sigma$是固定的，均值为训练阶段所有Batch均值的统计平均，方差为所有训练Batch方差的无偏估计，公式如下：
$$E[x]=E_{B}[\mu _B], Var[x]=\dfrac{m}{m-1}E_{B}[\sigma_B^2]$$
在测试阶段，BN变换式为
$$y=\dfrac{\gamma}{\sqrt{Var[x]+\varepsilon}}x+(\beta-\dfrac{\gamma E[x]}{\sqrt{Var[x]+\varepsilon}})$$

整个训练和测试流程如下：

BN变换置于网络激活函数层的前面，对于普通前馈神经网络，BN是对一层的每个神经元进行归一化处理；而在卷积神经网络中，BN则是对一层的每个特征图进行处理，类似于权值共享，一个特征图只有一对可学习参数$\gamma、\beta$，如果某一层的输入张量为$[batch\_size, height, width, channels]$，则BN变换是按照channels进行的，minibatch的大小相当于$batch\_size \times height \times width$。

有研究者认为，BN通过mini-batch来规范化某些层/所有层的输入，从而可以固定每层输入信号的均值与方差，实际上解决的并不是covariate shift的问题，因为均值方差一致的分布并不是同样的分布，ICS只是一种包装纸，BN实际解决的是梯度弥散的问题，在反向传播中，小于1的梯度值通过连乘操作会趋于0，而BN通过将每一层的输入规范为均值、方差一致，使得梯度传播较为稳定，在一定程度上避免了梯度消失的问题。

Advantage

总体来说，Batch Normalization主要有如下优点：

保证网络各层输入的均值和方差稳定（数据分布不一定一致？），减弱Internal Convariate Shift的影响
减小参数scale和初值对梯度的影响，解决了梯度爆炸或梯度消失的问题
在某种程度上实现了正则化，减弱对L2-norm、Dropout的依赖
让输入分布于饱和区域(Sigmoid)的概率降低
降低超参数选择对模型的影响，可使用较大的学习率加速训练