图像特征之Harris角点检测

发表于   |   分类于   |     |  

  角点检测(Corner Detection)也称为特征点检测，是图像处理和计算机视觉中用来获取图像局部特征点的一类方法，广泛应用于运动检测、图像匹配、视频跟踪、三维建模以及目标识别等领域中。

局部特征

  不同于HOG、LBP、Haar等基于区域(Region)的图像局部特征，Harris是基于角点的特征描述子，属于feature detector，主要用于图像特征点的匹配(match)，在SIFT算法中就有用到此类角点特征；而HOG、LBP、Haar等则是通过提取图像的局部纹理特征(feature extraction)，用于目标的检测和识别等领域。无论是HOG、Haar特征还是Harris角点都属于图像的局部特征，满足局部特征的一些特性。主要有以下几点：

  • 可重复性(Repeatability)：同一个特征可以出现在不同的图像中，这些图像可以在不同的几何或光学环境下成像。也就是说，同一物体在不同的环境下成像(不同时间、不同角度、不同相机等)，能够检测到同样的特征。
  • 独特性(Saliency)：特征在某一特定目标上表现为独特性，能够与场景中其他物体相区分，能够达到后续匹配或识别的目的。
  • 局部性(Locality)；特征能够刻画图像的局部特性，而且对环境影响因子(光照、噪声等)鲁棒。
  • 紧致性和有效性(Compactness and efficiency)；特征能够有效地表达图像信息，而且在实际应用中运算要尽可能地快。

相比于考虑局部邻域范围的局部特征，全局特征则是从整个图像中抽取特征，较多地运用在图像检索领域，例如图像的颜色直方图。
除了以上几点通用的特性外，对于一些图像匹配、检测识别等任务，可能还需进一步考虑图像的局部不变特征。例如尺度不变性(Scale invariance)和旋转不变性(Rotation invariance)，当图像中的物体或目标发生旋转或者尺度发生变换，依然可以有效地检测或识别。此外，也会考虑局部特征对光照、阴影的不变性。

Harris角点检测

  特征点在图像中一般有具体的坐标，并具有某些数学特征，如局部最大或最小灰度、以及某些梯度特征等。角点可以简单的认为是两条边的交点，比较严格的定义则是在邻域内具有两个主方向的特征点，也就是说在两个方向上灰度变化剧烈。如下图所示，在各个方向上移动小窗口，如果在所有方向上移动，窗口内灰度都发生变化，则认为是角点；如果任何方向都不变化，则是均匀区域；如果灰度只在一个方向上变化，则可能是图像边缘。

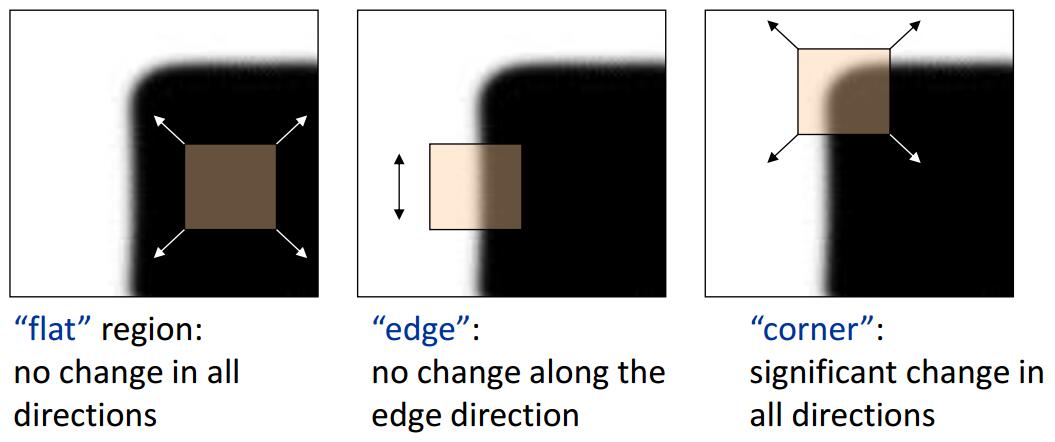
corner.jpg

  对于给定图像$I(x,y)$和固定尺寸的邻域窗口，计算窗口平移前后各个像素差值的平方和，也就是自相关函数
$$E(u,v)=\Sigma_x\Sigma_yw(x,y)[I(x+u,y+v)-I(x,y)]^2$$
其中，窗口加权函数$w(x,y)$可取均值函数或者高斯函数，如下图所示：

weights.jpg

根据泰勒展开，可得到窗口平移后图像的一阶近似
$$I(x+u,y+v)\approx I(x,y)+I_x(x,y)u+I_y(x,y)v$$
因此$E(u, v)$可化为
$$E(u,v) \approx \Sigma_{x,y}w(x,y)[I_x(x,y)u+I_y(x,y)v]^2=\left[u,v\right] M(x,y) \left[ \begin{matrix} u\\ v\end{matrix} \right]$$
$$M(x,y)=\Sigma_w \left[ \begin{matrix} I_x^2& I_xI_y \\ I_xI_y & I_y^2\end{matrix} \right] = \left[ \begin{matrix} A& C\\ C& B\end{matrix} \right]$$
$E(u,v)$可表示为一个二次项函数
$$E(u,v)=Au^2+2Cuv+Bv^2$$
其中$A=\Sigma_w I_x^2, B = \Sigma_w I_y^2, C=\Sigma_w I_x I_y$
二次项函数本质上是一个椭圆函数，椭圆的曲率和尺寸可由$M(x,y)$的特征值$\lambda_1,\lambda_2$决定，椭圆方向由$M(x,y)$的特征向量决定，椭圆方程和其图形分别如下所示：
$$\left[u,v\right] M(x,y) \left[ \begin{matrix} u\\ v\end{matrix} \right] = 1$$

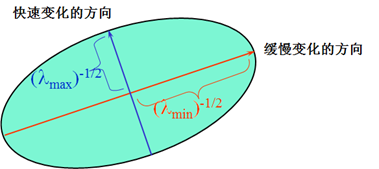
tuoyuan.png

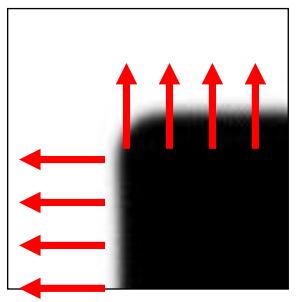
考虑角点的边界和坐标轴对齐的情况，如下图所示，在平移窗口内，只有上侧和左侧边缘，上边缘$I_y$很大而$I_x$很小，左边缘$I_x$很大而$I_y$很小，所以矩阵$M$可化简为
$$M=\left[ \begin{matrix} \lambda_1& 0\\ 0& \lambda_2\end{matrix} \right]$$

axis-aligned.jpg

当角点边界和坐标轴没有对齐时，可对角点进行旋转变换，将其变换到与坐标轴对齐，这种旋转操作可用矩阵的相似对角化来表示，即
$$M=X\Sigma X^T = X \left[ \begin{matrix} \lambda_1& 0\\ 0& \lambda_2\end{matrix} \right] X^T$$
$$Mx_i=\lambda_i x_i$$

not-aligned.jpg

  对于矩阵$M$，可以将其和协方差矩阵类比，协方差表示多维随机变量之间的相关性，协方差矩阵对角线的元素表示的是各个维度的方差，而非对角线上的元素表示的是各个维度之间的相关性，在PCA(主成分分析)中，将协方差矩阵对角化，使不同维度的相关性尽可能的小，并取特征值较大的维度，来达到降维的目的。类似的，可以将矩阵$M$看成是一个二维随机分布的协方差矩阵，通过将其对角化，求取矩阵的两个特征值，并根据这两个特征值来判断角点。

如下图所示，可根据矩阵$M$的特征值来判断是否为角点，当两个特征值都较大时为角点(corne)，一个特征值较大而另一个较小时则为图像边缘(edge)，两个特征值都较小时为均匀区域(flat)。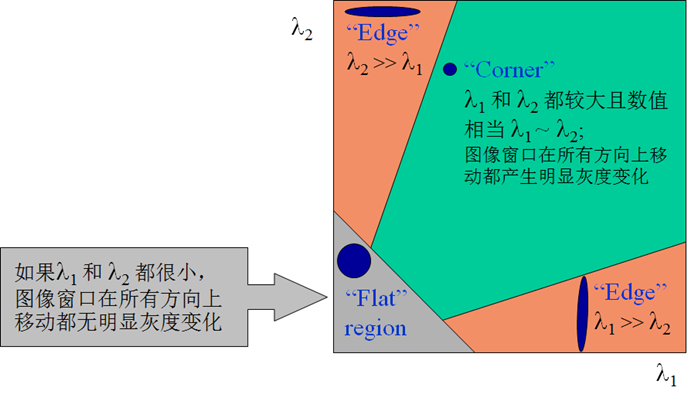
judge corners.png

在判断角点时，无需具体计算矩阵$M$的特征值，而使用下式近似计算角点响应值。
$$R = detM-\alpha (traceM)^2$$
$$detM=\lambda_1 \lambda_2=AB-C^2$$
$$traceM=\lambda_1 + \lambda_2 = A+B$$
式中，$detM$为矩阵$M$的行列式，$traceM$为矩阵$M$的迹，$\alpha$为一常数，通常取值为0.04~0.06。

算法实现

Harris角点检测的算法步骤归纳如下：

  • 计算图像$I(x,y)$在$X$方向和$Y$方向的梯度
    $$I_x=\dfrac {\partial I} {\partial x}=I(x,y)\otimes \left( \begin{matrix} -1& 0& 1\end{matrix} \right)$$
    $$I_y=\dfrac {\partial I} {\partial y}=I(x,y)\otimes \left( \begin{matrix} -1& 0& 1\end{matrix} \right)^T$$
  • 计算图像两个方向梯度的乘积$I_x^2、I_y^2、I_x I_y$
  • 使用窗口高斯函数分别对$I_x^2、I_y^2、I_x I_y$进行高斯加权，生成矩阵$M$。
  • 计算每个像素的Harris响应值$R$，并设定一阈值$T$，对小于阈值$T$的$R$置零。
  • 在一个固定窗口大小的邻域内($5 \times 5$)进行非极大值抑制，局部极大值点即为图像中的角点。

Harris角点性质

1.参数$\alpha$对角点检测的影响：增大$\alpha$的值，将减小角点响应值$R$，减少被检测角点的数量；减小$\alpha$的值，将增大角点响应值$R$，增加被检测角点的数量。
2.Harris角点检测对亮度和对比度的变化不敏感。

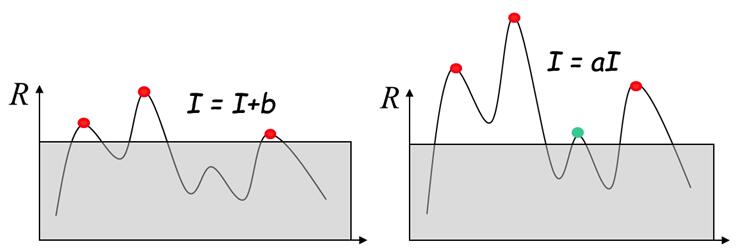
Brightness-Contrast.jpg

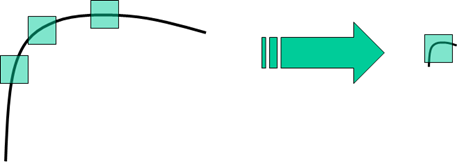
3.Harris角点检测具有旋转不变性，但不具备尺度不变性。如下图所示，在小尺度下的角点被放大后可能会被认为是图像边缘。

scale.png

Harris角点检测的结果示意图：

result.jpg

多尺度Harris角点检测

  Harris角点具有灰度不变性和旋转不变性，但不具备尺度不变性，而尺度不变性对于图像的局部特征来说至关重要。将Harris角点检测算子和高斯尺度空间表示相结合，可有效解决这个问题。与Harris角点检测中的二阶矩表示类似，定义一个尺度自适应的二阶矩
$$M=\mu (x,y,\sigma_I, \sigma_D)=\sigma_D^2g(\sigma_I) \otimes \left[ \begin{matrix} L_x^2(x,y,\sigma_D)& L_xL_y(x,y,\sigma_D)\\ L_xL_y(x,y,\sigma_D)& L_y^2(x,y,\sigma_D)\end{matrix} \right]$$
式中，$g(\sigma_I)$表示尺度为$\sigma_I$的高斯卷积核，$L_x(x,y,\sigma_D)$和$L_y(x,y,\sigma_D)$表示对图像使用高斯函数$g(\sigma_D)$进行平滑后取微分的结果。$\sigma_I$通常称为积分尺度，是决定Harris角点当前尺度的变量，$\sigma_D$为微分尺度，是决定角点附近微分值变化的变量，通常$\sigma_I$应大于$\sigma_D$。
算法流程：

  • 确定尺度空间的一组取值$\sigma_I=(\sigma_0, \sigma_1, \sigma_2,…, \sigma_n)=(\sigma, k\sigma, k^2\sigma,…, k^n\sigma), \sigma_D=s\sigma_I$
  • 对于给定的尺度空间值$\sigma_D$，进行角点响应值的计算和判断，并做非极大值抑制处理
  • 在位置空间搜索候选角点后，还需在尺度空间上进行搜索，计算候选点的拉普拉斯响应值，并于给定阈值作比较
    $$F(x,y,\sigma_n)=\sigma_n^2|L_{xx}(x,y,\sigma_n)+L_{yy}(x,y,\sigma_n)| \geq threshold$$
  • 将响应值$F$与邻近的两个尺度空间的拉普拉斯响应值进行比较，使其满足
    $$F(x,y,\sigma_n) > F(x,y,\sigma_l), l=n-1, n+1$$

这样既可确定在位置空间和尺度空间均满足条件的Harris角点。

reference