LoG(Laplacian of Gaussian)算子和DoG(Difference of Gaussian)算子是图像处理中实现极值点检测(Blob Detection)的两种方法。通过利用高斯函数卷积操作进行尺度变换,可以在不同的尺度空间检测到关键点(Key Point)或兴趣点(Interest Point),实现尺度不变性(Scale invariance)的特征点检测。
Laplacian of Gaussian(LoG)
Laplace算子通过对图像求取二阶导数的零交叉点(zero-cross)来进行边缘检测,其计算公式如下:
$$\nabla ^2 f(x,y)=\dfrac{\partial^2 f}{\partial x^2} + \dfrac{\partial^2 f}{\partial y^2}$$
由于微分运算对噪声比较敏感,可以先对图像进行高斯平滑滤波,再使用Laplace算子进行边缘检测,以降低噪声的影响。由此便形成了用于极值点检测的LoG算子。常用的二维高斯函数如下:
$$G_\sigma(x,y)=\dfrac{1}{\sqrt {2\pi \sigma ^{2}}} exp(-\dfrac{x^2+y^2}{2\sigma ^2})$$
原图像与高斯核函数卷积后再做laplace运算
$$\Delta [G_\sigma(x,y) \ast f(x,y)]=[\Delta G_\sigma(x,y)] \ast f(x,y)$$
$$LoG = \Delta G_\sigma(x,y)=\dfrac{\partial^2 G_\sigma(x,y)}{\partial x^2} + \dfrac{\partial^2 G_\sigma(x,y)}{\partial y^2}=\dfrac{x^2+y^2-2\sigma^2}{\sigma^4}e^{-(x^2+y^2)/2\sigma^2}$$
所以先对高斯核函数求取二阶导数,再与原图像进行卷积操作。由于高斯函数是圆对称的,因此LoG算子可以有效地实现极值点或局部极值区域的检测。
Difference of Gaussian(DoG)
DoG算子是高斯函数的差分,具体到图像中,就是将图像在不同参数下的高斯滤波结果相减,得到差分图。DoG算子的表达式如下:
$$DoG = G_{\sigma_1} - G_{\sigma_2}=\dfrac{1}{\sqrt{2\pi}} [\dfrac{1}{\sigma_1} e^{-(x^2+y^2)/2\sigma_1^2} - \dfrac{1}{\sigma_2} e^{-(x^2+y^2)/2\sigma_2^2}]$$
如果将高斯核函数的形式表示为
$$G_\sigma(x,y)=\dfrac{1}{2\pi \sigma ^{2}} exp(-\dfrac{x^2+y^2}{2\sigma ^2})$$
则存在以下等式
$$\dfrac{\partial G}{\partial \sigma} = \sigma \nabla ^2 G$$
$$\dfrac{\partial G}{\partial \sigma} \approx \dfrac{G(x,y,k\sigma)-G(x,y,\sigma)}{k\sigma-\sigma}$$
因此有
$$G(x,y,k\sigma)-G(x,y,\sigma) \approx (k-1)\sigma^2 \nabla ^2 G$$
其中$k-1$是个常数,不影响极值点的检测,LoG算子和DoG算子的函数波形对比如下图所示,由于高斯差分的计算更加简单,因此可用DoG算子近似替代LoG算子
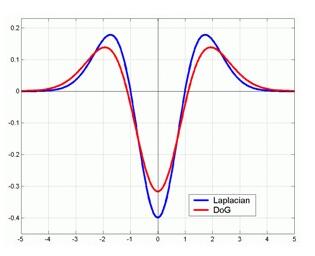
边缘检测(Edge Detection)和极值点检测(Blob Detection)
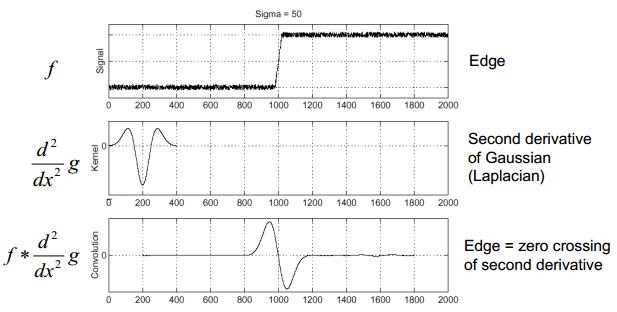
LoG算子和DoG算子既可以用于检测图像边缘,也可用于检测局部极值点或极值区域,图像边缘在LoG算子下的响应情况如下图所示,二阶微分算子在边缘处为一过零点,而且过零点两边的最大值(正)和最小值(负)的差值较大。
接下来观察下图,由边缘过渡到极值点,LoG算子的响应变化
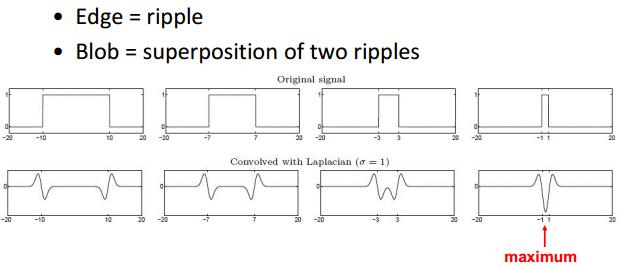
LoG算子在极值点(Blob)处的响应如下图所示:
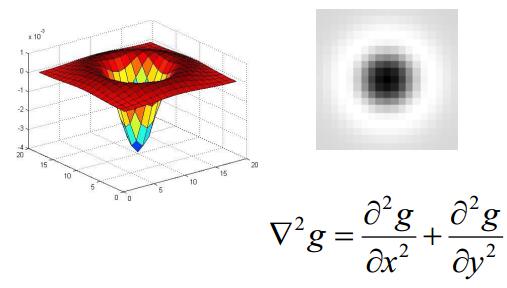
通过定义不同尺寸的高斯核函数,可以实现在不同尺度检测Blob,如下图所示
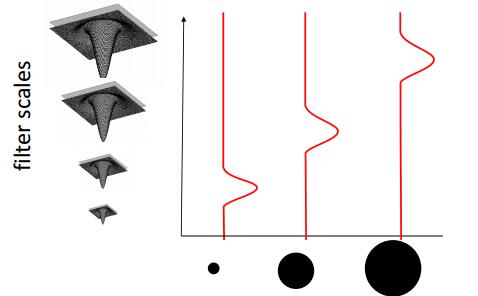
算法流程
- 对原图像进行LoG或者DoG卷积操作
- 检测卷积后图像中的过零点(边缘)或者极值点(Blob)
- 如果是检测边缘,则对过零点进行阈值化(过零点两边的最大值和最小值之间的差值要大于某个阈值);如果是检测极值点,则极值点的LoG或DoG响应值应该大于某个阈值。