图像特征描述子之BRISK

发表于   |   分类于   |     |  

  BRISK(Binary Robust Invariant Scalable Keypoints)是BRIEF算法的一种改进，也是一种基于二进制编码的特征描述子，而且对噪声鲁棒，具有尺度不变性和旋转不变性。

特征点检测

  BRISK主要利用FAST算法进行特征点检测，为了满足尺度不变性，BRISK构造图像金字塔在多尺度空间检测特征点。

构建尺度空间

  尺度空间包含n个octave($c_i$表示)和n个intro-octave($d_i$表示)，原论文中n=4。$c_0$是原始图像，$c_{i+1}$是$c_i$的降采样图像，缩放因子为2，即$c_{i+1}$的宽高分别为$c_i$的1/2；$d_0$是相对于原图缩放因子为1.5的降采样图像，同样，$d_{i+1}$是$d_i$的2倍降采样。$c_i$、$d_i$与原图像的大小关系如下表所示。

image $c_0$ $d_0$ $c_1$ $d_1$ $c_2$ $d_2$ $c_3$ $d_3$
width w 2w/3 w/2 w/3 w/4 w/6 w/8 w/12
height h 2h/2 h/2 h/3 h/4 h/6 h/8 h/12

由于n = 4，一共可以得到8张不同尺度的图像。在多尺度空间中，利用FAST9-16检测算子定位特征点，即在特征点邻域边界圆上的16个像素，至少有9个连续像素与特征点的灰度差值大于给定阈值T。此外，对原图像进行一次FAST5-8角点检测，作为$d_{-1}$层，方便后续在做非极大值抑制处理时，可以对相邻尺度空间的图像特征点进行比对。在前面博文中已详细介绍FAST角点检测。

非极大值抑制

  对多尺度空间的9幅图像进行非极大值抑制，与SIFT算法类似，在特征点的图像空间(8邻域)和尺度空间(上下两层18邻域)共26个邻域点做比较，FAST响应值须取得极大值，否则不能作为特征点。由于是在离散坐标空间中，特征点的位置比较粗糙，还需进一步精确定位。

亚像素精确定位

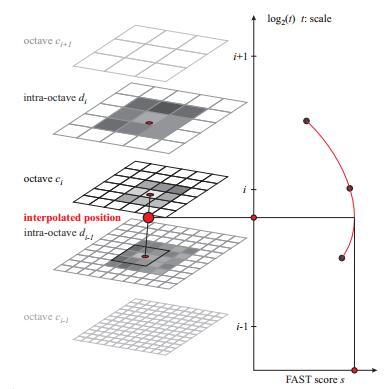
  得到图像特征点的坐标和尺度信息后，在极值点所在层及其上下层所对应的位置，对3个相应关键点的FAST响应进行二维二次函数插值(x,y方向)，得到二维平面精确的极值点位置和响应值后，再对尺度方向进行一维插值，得到特征点所对应的精确尺度。

multi-scale.jpg

特征点描述

  给定一组特征点(包含亚像素图像位置和浮点型尺度值)，BRISK通过比较邻域Patch内像素点对的灰度值，并进行二进制编码得到特征描述子。为了满足旋转不变性，需要选取合适的特征点主方向。

采样模式和旋转估计

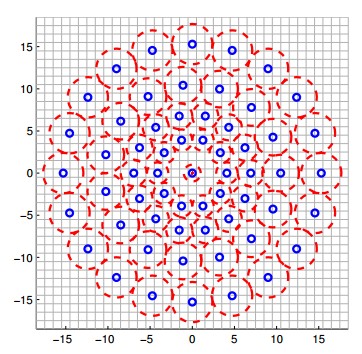
  特征点邻域的采样模式如下图所示，以特征点为中心，构建不同半径的同心圆，在每个圆上获取一定数目的等间隔采样点，所有采样点包括特征点一共有$N$个。由于这种采样模式会引起混叠效应，需要对所有采样点进行高斯滤波，滤波半径$r$和高斯方差$\sigma$成正比，同心圆半径越大，采样点滤波半径也越大。

sample pattern.jpg

$N$个采样点两两组合共有$\dfrac{N(N-1)}{2}$个点对，用集合$\cal A$表示，$I(p_i, \sigma_i)$为像素灰度值，$\sigma$表示尺度，用$g(p_i, p_j)$表示特征点局部梯度值，其计算公式为
$$g(p_i, p_j)=(p_j - p_i) \dfrac{I(p_j, \sigma_j) - I(p_i, \sigma_i)}{||p_j - p_i||^2}$$
采样点对的集合表示为
$$\cal A = \lbrace (p_i, p_j) \in R^2 \times R^2 | i < N \wedge j < i \rbrace $$
定义短距离点对子集$\cal S$和长距离点对子集$\cal L$
$$\cal S = \lbrace (p_i, p_j) \in \cal A | \left| p_j - p_i \right| < \sigma_{max} \rbrace \subseteq \cal A$$
$$\cal L = \lbrace (p_i, p_j) \in \cal A | \left| p_j - p_i \right| > \sigma_{min} \rbrace \subseteq \cal A$$
式中，阈值分别设置为$\sigma_{max} = 9.57t, \sigma_{min} = 13.67t$，$t$是特征点所在的尺度。特征点的主方向计算如下(此处仅用到了长距离点对子集)：
$$g = \left( \begin{matrix} g_x \\ g_y\end{matrix} \right) = \dfrac{1}{L} \Sigma_{p_i,p_j \in \cal L} g(p_i, p_j)$$
$$\alpha = arctan2(g_y, g_x)$$
长距离的点对均参与了运算，基于本地梯度互相抵消的假设，全局梯度的计算是不必要的。

生成描述子

  要解决旋转不变性，需要对特征点周围的采样区域旋转至主方向，得到新的采样区域，采样模式同上。采样点集合中包含$\dfrac{N(N-1)}{2}$个采样点对，考虑其中短距离点对子集中的512个点对，进行二进制编码，编码方式如下：
$$b = \begin{cases} 1,  I(p_j^\alpha, \sigma_j) > I(p_i^\alpha, \sigma_i) \\ 0,  otherwise \end{cases},   \forall (p_i^\alpha, p_j^\alpha) \in \cal S$$
$p_i^\alpha$表示旋转角度$\alpha$后的采样点。由此得到512bit也就是64Byte的二进制编码(BRISK64)。

特征点匹配

  BRISK特征匹配和BRIEF一样，都是通过计算特征描述子的Hamming距离来实现。

算法特点

  简单总结，BRISK算法具有较好的尺度不变性、旋转不变性，以及抗噪性能。在图像特征点的检测与匹配中，计算速度优于SIFT、SURF，而次于FREAK、ORB。对于较模糊的图像，能够取得较为出色的匹配结果。

Experiment & Result

OpenCV实现BRISK特征检测与描述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <opencv2/highgui/highgui.hpp>  
#include <opencv2/core/core.hpp>  
#include <opencv2/nonfree/features2d.hpp>  
#include <opencv2/nonfree/nonfree.hpp>  
  
using namespace cv;  
using namespace std;  
  
int main()  
{  
    //Load Image  
    Mat c_src1 =  imread( "1.png");  
    Mat c_src2 = imread("2.png");  
    Mat src1 = imread( "1.png", CV_LOAD_IMAGE_GRAYSCALE);  
    Mat src2 = imread( "2.png", CV_LOAD_IMAGE_GRAYSCALE);  
    if( !src1.data || !src2.data )  
    {  
        cout<< "Error reading images " << std::endl;  
        return -1;  
    }  
    //feature detect  
    BRISK detector;  
    vector<KeyPoint> kp1, kp2;     
    detector.detect( src1, kp1 );  
    detector.detect( src2, kp2 ); 
    //cv::BRISK extractor;  
    Mat des1,des2;//descriptor  
    detector.compute(src1, kp1, des1);  
    detector.compute(src2, kp2, des2);  
    Mat res1,res2;  
    int drawmode = DrawMatchesFlags::DRAW_RICH_KEYPOINTS;  
    drawKeypoints(c_src1, kp1, res1, Scalar::all(-1), drawmode);
    drawKeypoints(c_src2, kp2, res2, Scalar::all(-1), drawmode);  
     
    BFMatcher matcher(NORM_HAMMING);  
    vector<DMatch> matches;  
    matcher.match(des1, des2, matches);  
   
    Mat img_match;  
    drawMatches(src1, kp1, src2, kp2, matches, img_match);   
    imshow("matches",img_match);  
    cvWaitKey(0);  
    cvDestroyAllWindows();  
    return 0;  
}

result.jpg

OpenCV中BRISK算法的部分源码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
// construct the image pyramids
void BriskScaleSpace::constructPyramid(const cv::Mat& image)  
{  
  
  // set correct size:  
  pyramid_.clear();  
  
  // fill the pyramid:  
  pyramid_.push_back(BriskLayer(image.clone()));  
  if (layers_ > 1)  
  {  
    pyramid_.push_back(BriskLayer(pyramid_.back(), BriskLayer::CommonParams::TWOTHIRDSAMPLE)); 
  }  
  const int octaves2 = layers_;  
  
  for (uchar i = 2; i < octaves2; i += 2)  
  {  
    pyramid_.push_back(BriskLayer(pyramid_[i - 2], BriskLayer::CommonParams::HALFSAMPLE));//  
    pyramid_.push_back(BriskLayer(pyramid_[i - 1], BriskLayer::CommonParams::HALFSAMPLE));//  
  }  
}  
//extract the feature points 
void BriskScaleSpace::getKeypoints(const int threshold_, std::vector<cv::KeyPoint>& keypoints)  
{  
  // make sure keypoints is empty  
  keypoints.resize(0);  
  keypoints.reserve(2000);  
  
  // assign thresholds  
  int safeThreshold_ = (int)(threshold_ * safetyFactor_);  
  std::vector<std::vector<cv::KeyPoint> > agastPoints;  
  agastPoints.resize(layers_);  
  
  // go through the octaves and intra layers and calculate fast corner scores:  
  for (int i = 0; i < layers_; i++)  
  {  
    // call OAST16_9 without nms  
    BriskLayer& l = pyramid_[i];  
    l.getAgastPoints(safeThreshold_, agastPoints[i]);  
  }  
  
  if (layers_ == 1)  
  {  
    // just do a simple 2d subpixel refinement...  
    const size_t num = agastPoints[0].size();  
    for (size_t n = 0; n < num; n++)  
    {  
      const cv::Point2f& point = agastPoints.at(0)[n].pt;  
      // first check if it is a maximum:  
      if (!isMax2D(0, (int)point.x, (int)point.y))  
        continue;  
  
      // let's do the subpixel and float scale refinement:  
      BriskLayer& l = pyramid_[0];  
      int s_0_0 = l.getAgastScore(point.x - 1, point.y - 1, 1);  
      int s_1_0 = l.getAgastScore(point.x, point.y - 1, 1);  
      int s_2_0 = l.getAgastScore(point.x + 1, point.y - 1, 1);  
      int s_2_1 = l.getAgastScore(point.x + 1, point.y, 1);  
      int s_1_1 = l.getAgastScore(point.x, point.y, 1);  
      int s_0_1 = l.getAgastScore(point.x - 1, point.y, 1);  
      int s_0_2 = l.getAgastScore(point.x - 1, point.y + 1, 1);  
      int s_1_2 = l.getAgastScore(point.x, point.y + 1, 1);  
      int s_2_2 = l.getAgastScore(point.x + 1, point.y + 1, 1);  
      float delta_x, delta_y;  
      float max = subpixel2D(s_0_0, s_0_1, s_0_2, s_1_0, s_1_1, s_1_2, s_2_0, s_2_1, s_2_2, delta_x, delta_y);  
  
      // store:  
      keypoints.push_back(cv::KeyPoint(float(point.x) + delta_x, float(point.y) + delta_y, basicSize_, -1, max, 0));  
  
    }  
  
    return;  
  }  
  
  float x, y, scale, score;  
  for (int i = 0; i < layers_; i++)  
  {  
    BriskLayer& l = pyramid_[i];  
    const size_t num = agastPoints[i].size();  
    if (i == layers_ - 1)  
    {  
      for (size_t n = 0; n < num; n++)  
      {  
        const cv::Point2f& point = agastPoints.at(i)[n].pt;  
        // consider only 2D maxima...  
        if (!isMax2D(i, (int)point.x, (int)point.y))  
          continue;  
  
        bool ismax;  
        float dx, dy;  
        getScoreMaxBelow(i, (int)point.x, (int)point.y, l.getAgastScore(point.x, point.y, safeThreshold_), ismax, dx, dy);  
        if (!ismax)  
          continue;  
  
        // get the patch on this layer:  
        int s_0_0 = l.getAgastScore(point.x - 1, point.y - 1, 1);  
        int s_1_0 = l.getAgastScore(point.x, point.y - 1, 1);  
        int s_2_0 = l.getAgastScore(point.x + 1, point.y - 1, 1);  
        int s_2_1 = l.getAgastScore(point.x + 1, point.y, 1);  
        int s_1_1 = l.getAgastScore(point.x, point.y, 1);  
        int s_0_1 = l.getAgastScore(point.x - 1, point.y, 1);  
        int s_0_2 = l.getAgastScore(point.x - 1, point.y + 1, 1);  
        int s_1_2 = l.getAgastScore(point.x, point.y + 1, 1);  
        int s_2_2 = l.getAgastScore(point.x + 1, point.y + 1, 1);  
        float delta_x, delta_y;  
        float max = subpixel2D(s_0_0, s_0_1, s_0_2, s_1_0, s_1_1, s_1_2, s_2_0, s_2_1, s_2_2, delta_x, delta_y);  
  
        // store:  
        keypoints.push_back(cv::KeyPoint((float(point.x) + delta_x) * l.scale() + l.offset(), (float(point.y) + delta_y) * l.scale() + l.offset(), basicSize_ * l.scale(), -1, max, i));  
      }  
    }  
    else  
    {  
      // not the last layer:  
      for (size_t n = 0; n < num; n++)  
      {  
        const cv::Point2f& point = agastPoints.at(i)[n].pt;  
  
        // first check if it is a maximum:  
        if (!isMax2D(i, (int)point.x, (int)point.y))  
          continue;  
  
        // let's do the subpixel and float scale refinement:  
        bool ismax=false;  
        score = refine3D(i, (int)point.x, (int)point.y, x, y, scale, ismax);  
        if (!ismax)  
        {  
          continue;  
        }  
  
        // finally store the detected keypoint:  
        if (score > float(threshold_))  
        {  
          keypoints.push_back(cv::KeyPoint(x, y, basicSize_ * scale, -1, score, i));  
        }  
      }  
    }  
  }  
}

reference