链表问题集锦（一）

发表于   |   分类于   |     |  

将数据结构中一些经典的链表问题做一个总结归纳。

单链表结点定义：

1
2
3
4
5
struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(NULL) {}
};

在O(1)时间内删除指定链表结点

题目描述：给定链表的头指针和一个结点指针，在O(1)时间内删除该结点。
分析：一般做法是借助两个指针p1、p2（一前一后），从头开始遍历，直到后一个指针p2和待删除结点相同，然后使p1->next=p2->next，并释放掉p2结点。但此处强调是O(1)时间，因此可直接将待删除结点p的值替换为下一个结点的值，并使p->next=p->next->next，并删除下一个结点。当然前提是待删除结点不能是尾结点，即其下一个结点不能为空。

1
2
3
4
5
6
7
8
9
void deleteNode(ListNode *node)
{
    if(!node || !node->next)
    	return;
    ListNode* pNext = node->next;
    node->val = pNext->val;
    node->next = pNext->next;
    delete pNext;
}

求链表倒数第k个结点

题目描述：给定一个单链表，找到倒数第k个结点（或移除该结点），例如链表 1->2->3->4->5，k = 2，则倒数第k个结点值为4，移除该结点后，链表为1->2->3->5。LeetCode
分析：借助快慢两个指针fast、slow，首先fast先正向移动到第n个结点，然后两个指针同步移动，直至fast指针为空（走到链表末尾），此时slow指针所指向的即是倒数第k个结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
//找到倒数第n个结点
ListNode* findNthFromEnd(ListNode* head, int n)
{
    if(n < 0)   return NULL;
    ListNode *slow = head, *fast = head;
    for(int i = 0; i < n && fast; i++)
    {
    	fast = fast->next;
    }
    if(i < n)   return NULL;
    while(fast)
    {
    	slow = slow->next;
    	fast = fast->next;
    }
    return slow;
}
//删除倒数第n个结点
ListNode* removeNthFromEnd(ListNode* head, int n) 
{
    if(n < 0)	return NULL;
    ListNode* start = new ListNode(0);	//加一个起始（首）结点可有效解决只有一个元素的情况
    ListNode *front = start, *back = start;
    back->next = head;
    for(int i = 0; i < n + 1 && front; i++)
    {
        front = front->next;
    }
    if(i < n + 1)   return NULL;
    while(front)
    {
        front = front->next;
        back = back->next;
    }
    front = back->next;
    back->next = back->next->next;
    free(front);
    return start->next;
}

求链表的中间节点

题目描述：求链表的中间结点，如果链表长度为奇数，则返回中间结点；若为偶数，则返回中间两个结点中的任意一个。
分析：一般思路是先完整遍历一次链表，求得整个链表的长度，然后长度取半，再从头开始移动指针，即可定位到中间结点。如果只允许遍历一次链表的话，可通过两个指针完成，两个指针均从头部结点开始，一个每次移动一步，另一个每次移动两步，这样快指针走到链表末尾时，慢指针刚好指向中间结点。

1
2
3
4
5
6
7
8
9
10
11
12
ListNode* findMiddleNode(ListNode* head)
{
    if(head == NULL)    return NULL;
    ListNode *slow = head, *fast = head;
    //while(fast->next && fast->next->next)	//对于链表长度为偶数的情况，返回中间两个结点中的第一个
    while(fast && fast->next)	//对于链表长度为偶数的情况，返回中间两个结点中的第二个
    {
    	fast = fast->next->next;
    	slow = slow->next;
    }
    return slow;
}

判断单链表是否存在环

题目描述：输入一个单链表，判断链表是否存在环。LeetCode
分析：借助两个指针，分别从头结点出发，一个指针每次移动一个步长，另一个指针每次移动两个步长，如果存在环，则两个指针必在环内相遇。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
bool hasCycle(ListNode *head) 
{
    if(!head || !head->next)
        return false;
    ListNode *p1, *p2;
    p1 = p2 = head;
    while(p2 && p2->next)
    {
        p1 = p1->next;
        p2 = p2->next->next;
        if(p1 == p2)  
            return true;
    }
    return false;
}

找到单链表成环的入口点

题目描述，如果单链表存在环，则找到环的入口点，若不存在，则返回NULL。LeetCode
分析：借助两个指针，分别从头结点出发，一个指针每次移动一个步长，另一个指针每次移动两个步长，如果存在环，则两个指针必在环内相遇。然后一个指针指向链表头结点，另一个指针仍位于相遇点，两个指针均以单步长移动，再次相遇点即为环的起始点。设第一次相遇点距离链表起点为k，环起始点距离链表起点为s，环起始点到第一次相遇点距离为m，环长度为r，则有k = s + m, 且2k - k = nr = k, 即 s = nr - m。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
ListNode *detectCycle(ListNode *head) 
{
    if(!head || !head->next)
        return NULL;
    ListNode *p1, *p2;
    p1 = p2 = head;
    bool flag = false;
    while(p2 && p2->next)
    {
        p1 = p1->next;
        p2 = p2->next->next;
        if(p1 == p2)  
        {
            flag = true;
            break;
        }
    }
    if(!flag)   return NULL;
    
    p1 = head;
    while(p1 != p2)
    {
        p1 = p1->next;
        p2 = p2->next;
    }
    return p1;
}

判断两个链表是否相交

题目描述：给定两个单链表（不带环），判断是否相交

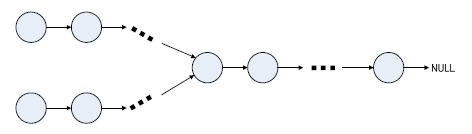
linkedlist.jpg

分析：
1.使用两重循环判断一个链表的某个结点是否在另一个链表中，时间复杂度为O(n*m)
2.针对第一个链表构造hash表，然后遍历第二个链表，判断第二个链表是否有结点在hash表中，时间复杂度为O(n+m)，空间复杂度为O(n)
3.转换为环的问题：把第二个链表连接到第一个链表后面，如果得到的链表有环，则说明两链表相交，判断是否有环可借助上面的方法。这里可使用更简单的方法，如果有环，则第二个链表的表头也在环上，即构成一个循环链表，因此只需要遍历第二个链表，看是否回到起始点即可判断，时间复杂度为线性，空间复杂度为O(1)
4.如果两个没有环的链表相交于一点，那这个结点之后的所有结点都是共有的，包括最后一个结点，因此只需要分别遍历两个链表至最后一个结点，判断是否相等，即可确定两链表是否相交，时间复杂度为线性，空间复杂度为O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
bool isIntersectOfTwoLinkedList(ListNode* head1, ListNode* head2)
{
    if(!head1 || !head2)	
    	return false;
    while(head1->next)
    	head1 = head1->next;
    while(head2->next)
    	head2 = head2->next;
    if(head1 == head2)
    	return true;
    else
    	return false;
}

两链表相交的第一个公共结点

题目描述：如果两个无环单链表相交，求出相交结点
分析：采用对齐的思想，分别遍历两个链表，得到其长度L1、L2，采用两个指针分别指向两个链表的头部，然后将较长链表的指针移动L2-L1个结点（假设L2>L1），再同时向后移动两指针，直到两指针相等即为相交结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
ListNode* findIntersectNode(ListNode* head1, ListNode* head2)
{
    int len1 = 0, len2 = 0;
    ListNode *pNode1 = head1, *pNode2 = head2;
    while(pNode1)
    {
    	len1++;
    	pNode1 = pNode1->next;
    }
    while(pNode2)
    {
    	len2++;
    	pNode2 = pNode2->next;
    }
    pNode1 = head1;
    pNode2 = head2;
    if(len1 > len2)
    {
    	for(int i = 0; i < len1 - len2; i++)
    	   pNode1 = pNode1->next;
    }
    else
    {
    	for(int i = 0; i < len2 - len1; i++)
    	   pNode2 = pnode2->next;
    }
    while(pNode1)
    {
    	if(pNode1 == pNode2)
    	   return pNode1;
    	pNode1 = pNode1->next;
    	pNode2 = pNode2->next;
    }
    return NULL;
}

如果两链表有环，判断是否相交

分析：如果两个链表有环且相交，则两个链表共有一个环，即环上的任意一个结点都存在与两个链表上，因此只需要判断一个链表的环起始点是否在另外一个链表（的环）上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
ListNode* hasCycle(ListNode *head) 
{
    if(!head || !head->next)
        return NULL;
    ListNode *p1, *p2;
    p1 = p2 = head;
    while(p2 && p2->next)
    {
        p1 = p1->next;
        p2 = p2->next->next;
        if(p1 == p2)  
            return p1;
    }
    return NULL;
}
bool isIntersectWithLoop(ListNode* head1, ListNode* head2)
{
    ListNode *pNode1, *pNode2;
    pNode1 = hasCycle(head1);
    pNode2 = hasCycle(head2);
    if(!pNode1 || !pNode2)
    	return false;
    if(pNode1 == pNode2)
    	return true;
    ListNode* pNode = pNode2->next;
    while(pNode != pNode2)
    {
    	if(pNode == pNode1)
    	   return true;
    	pNode = pNode->next;
    }
    return false;
}